Fonction bizarre
Olympiades mathématiques, énigmes et défis
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 03 Jan 2019, 19:29
salut
Partie A
On considère la fonction f de [0;
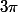
} dans
définie par:
si x appartient à [0;2
] alors f(x)=x+sin(x)
La partie bleue du graphe de f est l'image de la partie rouge du graphe par l'homothétie de centre A et de rapport -1/2
Soit un point M(x;y) de la partie bleue du graphe de f.
Exprimer y en fonction de x ( x appartient à {
;
])
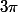
Partie B
On définit la fonction f de [0,
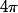
] dans
on continuant indéfiniment à effectuer les homothéties et en posant f(4
)=4
f est-elle continue, dérivable, strictement croissante sur [0;
] ?
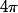
sujet inspiré par
superieur/bijectivite-sin-t202653.html
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
par FLBP » 03 Jan 2019, 20:21
Salut,
Avant que je continue trop loin, est que cette fonction est correcte pour
?
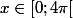
 = x + 2^{-g(x)} \sin(2^{g(x)} x))
avec
 = \lfloor \log_{\frac{1}{2}}(1-\frac{x}{4 \pi}) \rfloor -1)
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 04 Jan 2019, 09:38
Salut
On peut montrer par récurrence que:
Sur chaque intervalle
,4\pi(1-\frac{1}{2^{n+1}})])
=x+\frac{sin(2^n x)}{2^n })
soit
sur
,
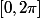
=x+sin(x))
sur
,
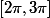
=x+\frac{sin(2 x)}{2})
sur
,
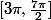
=x+\frac{sin(2^2 x)}{2^2 })
etc
Ca revient sans doute au même que ce que tu as fait.
-
FLBP
- Habitué(e)
- Messages: 289
- Enregistré le: 25 Aoû 2017, 01:07
-
par FLBP » 04 Jan 2019, 10:23
D'accord merci,
Sinon, questions continuité et dérivabilité, ça à l'air de coller; les points critiques étant les centres d’homothétie:
} \frac{\rm d}{\rm dx}(x + \frac{\sin(2^n x)}{2^n}) = \lim_{x \to 4 \pi (1 - \frac{1}{2^{n+1}})}1 + \cos(2^n x) = 2 = \lim_{x \to 4 \pi (1 - \frac{1}{2^{n+1}})} \frac{\rm d}{\rm dx}(x + \frac{\sin(2^{n+1} x)}{2^{n+1}}))
Sinon, pour la croissance, avec l'expression précédente :
}{2^n}) = 1 + \cos(2^n x) \geq 0)
La pente ne sera jamais négative sur l'intervalle
-
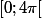
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 04 Jan 2019, 10:32
je pense que f n'est pas dérivable en 4 (à gauche) mais elle est continue et strictement croissante sur [0;4
] et dérivable sur [0;
[
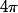
Ci-dessous la courbe en utilisant une séquence avec geogebra (101 "morceaux")
on peut zoomer sur A
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
