Comment factoriser, en utilisant au maximum des outils de seconde/première, les deux polynômes:
[Défi Lycée] - Factorisations
26 messages
- Page 1 sur 2 - 1, 2
[Défi Lycée] - Factorisations
Bonjour,
Comment factoriser, en utilisant au maximum des outils de seconde/première, les deux polynômes:
 = 1 + X + X^8)
 = 1 + X^5 + X^{10})
Comment factoriser, en utilisant au maximum des outils de seconde/première, les deux polynômes:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: [Défi Lycée] - Factorisations
bjr
pour Q(x) on peut poser U=x^5
Q(U)=1+U+U²
facile à resoudre dans les complexes pour mettre en facteurs
que l'on peut aussi utiliser dans P(u)=(1+u+u²)(1-u²+u^3 -u^5+u^6)
pour Q(x) on peut poser U=x^5
Q(U)=1+U+U²
facile à resoudre dans les complexes pour mettre en facteurs
que l'on peut aussi utiliser dans P(u)=(1+u+u²)(1-u²+u^3 -u^5+u^6)
Re: [Défi Lycée] - Factorisations
Bonjour,
Les complexes ne sont pas connus en première/seconde
Il faut aussi extraire des racines cinquièmes de complexes puis les regrouper.
Par contre pour P, le changement de variable que tu proposes ne marche pas
Les complexes ne sont pas connus en première/seconde
Il faut aussi extraire des racines cinquièmes de complexes puis les regrouper.
Par contre pour P, le changement de variable que tu proposes ne marche pas
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: [Défi Lycée] - Factorisations
c'est une méthode rigoureuse ou du tatonnement aidé?
Parce que pour x=1 cela fait 3 donc les produits de facteur vont faire 3
pour x= -1 cela fait 1
voilà qui limite un peu ce que l'on peut mettre dedans
sachant qu'aux deux bouts on a bien envie de faire du 1 x 1 = 1
et x^8 = x puissance 7 fois x puissance 1
ou 6 et 2 ou 5 et 3 ou 4 et 4
Pas bien regardé si cela fait encore beaucoup de choix?
Parce que pour x=1 cela fait 3 donc les produits de facteur vont faire 3
pour x= -1 cela fait 1
voilà qui limite un peu ce que l'on peut mettre dedans
sachant qu'aux deux bouts on a bien envie de faire du 1 x 1 = 1
et x^8 = x puissance 7 fois x puissance 1
ou 6 et 2 ou 5 et 3 ou 4 et 4
Pas bien regardé si cela fait encore beaucoup de choix?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: [Défi Lycée] - Factorisations
salut
c'est un peu artificiel, mais bon
On "complète":

-x^2(1+x+x^2)+x^3(1+x+x^2)-x^5(1+x+x^2)+x^6(1+x+x^2))
(1-x^2+x^3-x^5+x^6))
ou alors, on voit que j et j² annulent P (pour terminales et plus)
c'est un peu artificiel, mais bon
On "complète":
ou alors, on voit que j et j² annulent P (pour terminales et plus)
Re: [Défi Lycée] - Factorisations
y a t-il un rapport avec le fait que cela marche pour:
x^17 + x^10 + 1
x^13 + x¨14 + 1
x^58 + x^29 + 1
......
enfin plenty of qui ressemblent.
x^17 + x^10 + 1
x^13 + x¨14 + 1
x^58 + x^29 + 1
......
enfin plenty of qui ressemblent.
Modifié en dernier par beagle le 07 Nov 2017, 14:49, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: [Défi Lycée] - Factorisations
et les cousins germains:
x^26 + x^16 + 1
x^32 + x^22 + 1
x^154 + x^38 +1
....
x^26 + x^16 + 1
x^32 + x^22 + 1
x^154 + x^38 +1
....
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: [Défi Lycée] - Factorisations
Salut
c'est un peu artificiel, mais bon
On "complète":
ou alors, on voit que j et j² annulent P (pour terminales et plus)
C'est un peu comme faire une division euclidienne par 1+x+x^2.
Mais après comment peut-on au lycée savoir que la factorisation est finie? La méthode ne le dit pas.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: [Défi Lycée] - Factorisations
beagle a écrit:y a t-il un rapport avec le fait que cela marche pour:
x^17 + x^10 + 1
x^13 + x¨14 + 1
x^58 + x^29 + 1
......
enfin plenty of qui ressemblent.
Oui mais il faut aller chercher des critères d'irréductibilités (Eisenstein et compagnie) pour en tirer quelque chose de général pour trouver des briques élémentaires ou des simplifications miraculeuses.
Mais pas facile avec des outils rustiques.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: [Défi Lycée] - Factorisations
J'ai trouvé la filmographie d' Eisenstein, mais alors dans quel film il a expliqué ça, ptain je suis pas rendu!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: [Défi Lycée] - Factorisations
Bonsoir Lostounet,
En 1ère pour savoir que la factorisation s'arrête à 1+x+x^2, c'est facile : delta. Sauf qu'on ne sait pas très bien que : une ou des racines implique factorisable
Pour savoir qu'un polynôme de degré supérieur est factorisable, on peut toujours chercher ses racines en étudiant la fonction : dérivée première, seconde... à condition que le degré ne soit pas trop élevé, et sauf même remarque. Sans compter que le polynôme peut être factorisable sans racine réelle : X^4+X^2+1.
En 1ère pour savoir que la factorisation s'arrête à 1+x+x^2, c'est facile : delta. Sauf qu'on ne sait pas très bien que : une ou des racines implique factorisable
Pour savoir qu'un polynôme de degré supérieur est factorisable, on peut toujours chercher ses racines en étudiant la fonction : dérivée première, seconde... à condition que le degré ne soit pas trop élevé, et sauf même remarque. Sans compter que le polynôme peut être factorisable sans racine réelle : X^4+X^2+1.
Re: [Défi Lycée] - Factorisations
oui mais comment on explique au lycée que cela marche toujours super bien, (enfin dès qu'on a reperé un petit truc):
x^154 + x^149 + 1
x^131 + x^76 + 1
....
dans ces cassis deux produits de facteur = le deuxième ne peut pas ètre refactorisé
x^154 + x^149 + 1
x^131 + x^76 + 1
....
dans ces cassis deux produits de facteur = le deuxième ne peut pas ètre refactorisé
Modifié en dernier par beagle le 07 Nov 2017, 19:53, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: [Défi Lycée] - Factorisations
Pseuda a écrit:Bonsoir Lostounet,
En 1ère pour savoir que la factorisation s'arrête à 1+x+x^2, c'est facile : delta. .
Bonjour
Tu veux faire delta pour un polynôme de degré 6 ? :p
Je demandais comment savoir qu'on ne peut pas scinder le polynôme de degré 6 qui reste. Pour le 1+x+x^2 j'accepte la proposition.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: [Défi Lycée] - Factorisations
Bon alors il ya une serie avec deux facteurs,
mais la série que j'ai mise avec les ordres pairs est en 3 facteurs, n'est-ce pas,
donc dans un cas le deuxième facteur n'est pas refactorisable
et dans un cas oui:
x^122 + x^112 + 1
x^76 + x^134 + 1
là on peut refactoriser (donc 3 produits de facteur)
mais pour comprendre faut aller au lycée.
Vous savez quel lycée je dois aller pour comprendre ça?
je demande à voir qui? Et de la part de qui?
mais la série que j'ai mise avec les ordres pairs est en 3 facteurs, n'est-ce pas,
donc dans un cas le deuxième facteur n'est pas refactorisable
et dans un cas oui:
x^122 + x^112 + 1
x^76 + x^134 + 1
là on peut refactoriser (donc 3 produits de facteur)
mais pour comprendre faut aller au lycée.
Vous savez quel lycée je dois aller pour comprendre ça?
je demande à voir qui? Et de la part de qui?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: [Défi Lycée] - Factorisations
@Lostounet Non delta que pour le degré 2  Sinon pour le polynôme de degré 6, je ne vois rien sans aide au lycée.
Sinon pour le polynôme de degré 6, je ne vois rien sans aide au lycée.
Re: [Défi Lycée] - Factorisations
pour revenir au problème posé, on peut factoriser Q à partir de la factorisation de P
+(1-x^2-x^3+x^5))
la seconde parenthèse vaut-x^3(1-x^2)=(1-x^2)(1-x^3)=(1-x^2)(1-x)(1+x+x^2))
on a donc
(1-x^2+x^3-x^5+x^6)+(1-x^2)(1-x)(1+x+x^2))
on factorise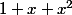
=(1+x+x^2)(1-x+x^3-x^4+x^5-x^7+x^8))
la seconde parenthèse vaut
on a donc
on factorise
Re: [Défi Lycée] - Factorisations
Bonjour
On peut remarquer que Q(x)=(1+x^5+x^10) admet une factorisation de la forme
=\Pi_{k=1}^5 (1+x^2+a_i x)) avec après calculs
avec après calculs
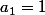
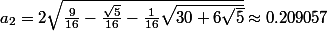
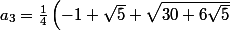\approx 1.9563)
 \left(\frac{7}{16}-\frac{\sqrt{5}}{16}-\frac{1}{8} \sqrt{\frac{3}{2} \left(5-\sqrt{5}\right)}\right)}-\frac{1}{8} \left(1+\sqrt{5}\right) \left(-1+\sqrt{5}+\sqrt{30+6 \sqrt{5}}\right)\right)\approx -1.82709)
 \sqrt{\frac{9}{16}-\frac{\sqrt{5}}{16}-\frac{1}{16} \sqrt{30+6 \sqrt{5}}}+\sqrt{\frac{15}{64}-\frac{\sqrt{5}}{64}+\frac{5}{128} \sqrt{30+6 \sqrt{5}}-\frac{1}{128} \sqrt{5 \left(30+6 \sqrt{5}\right)}}\right)\approx -1.33826)
mais visiblement ce n'est plus du niveau collège.
Par contre je ne sais pas s'il est possible de trouver la décomposition de P(x). C'est à voir.
Pourquoi ne pas proposer=1+x^4+x^8)
et ça on peut le faire au collège:
=\left(1-x+x^2\right) \left(1+x+x^2\right) \left(1-\sqrt{3} x+x^2\right)\left(1+\sqrt{3} x+x^2\right))
On peut remarquer que Q(x)=(1+x^5+x^10) admet une factorisation de la forme
mais visiblement ce n'est plus du niveau collège.
Par contre je ne sais pas s'il est possible de trouver la décomposition de P(x). C'est à voir.
Pourquoi ne pas proposer
et ça on peut le faire au collège:
Re: [Défi Lycée] - Factorisations
Lostounet a écrit:Je demandais comment savoir qu'on ne peut pas scinder le polynôme de degré 6 qui reste. Pour le 1+x+x^2 j'accepte la proposition.
Bonjour,
D'ailleurs, le polynôme de degré 6 est factorisable ? On le sait dans le supérieur. Mais sait-on le factoriser ? Avec la méthode d'@aviateur ?
Par contre, si on sait que le polynôme est factorisable (par exemple car on a reconnu des racines complexes conjuguées), on peut tjs faire la division euclidienne (niveau lycée aidé) ou recherche des coefficients par identification.
Mais sauf cas particuliers, je ne vois pas.
Re: [Défi Lycée] - Factorisations
Pseuda a écrit:
Par contre, si on sait que le polynôme est factorisable (par exemple car on a reconnu des racines complexes conjuguées), on peut tjs faire la division euclidienne (niveau lycée aidé) ou recherche des coefficients par identification.
Mais sauf cas particuliers, je ne vois pas.
oui, pour factoriser complètement P, il faudrait pouvoir calculer les réels
Du calcul en vue, on dirait ...
Re: [Défi Lycée] - Factorisations
beagle a écrit:y a t-il un rapport avec le fait que cela marche pour:
x^17 + x^10 + 1
x^13 + x¨14 + 1
x^58 + x^29 + 1
......
enfin plenty of qui ressemblent.
Bonjour Beagle,
Il y a un rapport en effet. En fait tous les polynômes du type
J'imagine qu'on peut en fabriquer plein du même genre, avec les racines quatrièmes, cinquièmes,... de 1 !
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
