Facile et simple ne sont pas confondus

[Arbre]

Finalement, j'arrive (avec environs 5 minutes de calcule à donner)



Donc @Pascale : à 0.2 prés tu es bon, mais je demande la troncature à 0.001 prés.

[Arbre]

@la modération mon nombre de vues est bloqué à 1547

[pascal16]

pour la 36
cos (2a)=2cos²(a)-1

soit la suite

sqrt(1-(U_2017)²)=0.5116...

j'ai pas le signe, mai je vois pas mon erreur (il y a suffisamment peu de termes pour que les erreurs de calculs ne soient pas en cause)

programme small basic :
u=math.cos(1)
For i=2 To 2017
u=2*u*u-1
EndFor
u=math.SquareRoot(1-u*u)
TextWindow.Write(u)

PS : je vois 1548 moi

[Arbre]

Non, cela ne marche pas pour cela il te faudrait une valeur approchée de cos(1) à au moins , en effet chaque fois que tu éléves aux carrés ou multiplies par deux tu diminues la précision.

Pour t'en convaincre change cos(1) par cos(1)+ 10^{-10} et tu verras que ton calcule changera de beaucoup.

PS : dans les autres conversations aprés une visite le compteur de vue s'incrèmente de un, ici non, il faut attendre plusieurs vues pour cela, fait l'expérience tu verras.

[pascal16]

j'ai essayé en ne bougeant que de 10^-25, c'est pas bon non plus. avec seulement 2017 boucles, je ne pensais pas avoir autant d'erreur. Il faudrait une précision de 10^-610 environ...

l'autre piste était de retirer 2pi autant de fois que possible

un autre, de faire un DL après modif de la fonction

[Arbre]

effectivement j'ai fait le calcul avec une précision de

Mais il y a deux problème technique à résoudre :

1/Comment calculer cos(1) et sin(1) avec cette précision.

2/Comment faire le calcul pour ne pas perdre la précision et ne pas être dépassé par la taille des nombres à gérer.

[aviateur]

@arbre,
Peux tu Justifier avec rigueur les valeurs que tu donnes pour sin(2^1000) et pour sin(2^2017)?
Je devine bien que la première vient de ton logiciel mais est ce que la valeur fournie est correcte?
Pour sin(2^2017) elle vient d'où?

[pascal16]

la preuve ultime : google
Je ne sais pas comment il fait pour ne pas saturer
1024 remplace 2^10, y en a 200 par plusieurs copier-coller soit 2^10^200=2^2000
puis *1024 pour faire 2^2010
puis *128 pour faire 2^2017



j'ai recherché des formules de sin(a²), mais j'ai rien trouvé dessus

PS : la réponse est fausse, la calculatrice tourne avec des réels double précision, donc tronqués rapidement

[Arbre]

Bonjour,

@Aviateur : pour montrer que la précision suffisait, j'ai changé la précision pour vérifier la stabilité du résultat, le système étant cahotique c'est stabilité m'assure que j'ai la bonne valeur.

@Pascal : essai de résoudre les 2 difficultés techniques que je donne , alors la solution sera à porter de programme.

1/Comment calculer cos(1) et sin(1) avec cette précision.
2/Comment faire le calcul pour ne pas perdre la précision et ne pas être dépassé par la taille des nombres à gérer.

Pour se faire j'ai utilisé des BigInteger.

[aviateur]

@aviateur : pour montrer que la précision suffisait, j'ai changé la précision pour vérifier la stabilité du résultat, le système étant cahotique c'est stabilité m'assure que j'ai la bonne valeur

.

@arbre Je ne suis toujours pas d'accord avec ta réponse dont les arguments sont insuffisants d'un point de vue scientifique. C'est trop vague à mon avis.
Je devine que tu calcules (comme @pascal le fait aussi par ailleurs) la valeur sin(2^2017) par itérations et le problème étant instable (ici c'est l'effet papillon) vous obtenez un résultat avec une précision amplifiée de 2^2000 environ.
Ce qui veut dire que votre résultat est complètement à côté de la plaque.
d'autre part, tu dois justifier correctement que si tu obtiens 2 résultats identiques avec 2 précisions différentes demandées à l'ordinateur que cela implique que le résultat obtenu est bon.

[Arbre]

Alors tant que tu y es pourquoi ne pas justifier aussi les fonctions déjà implanté que j'utilise, car elles n'ont pas de preuves de sécurités.

Bon enfin bref, j'ai fait le calcul et j'ai un moyen de le confirmé basta, si à chaque fois que je change la précision j'obtiens le même résultat, si je fais cela n fois en prenant des précisions de plus en plus grandes, alors on peut dire avec une proba de que le résultat est bon, mais c'est vrai je n'aurais pas 100%, mais en math on n'a jamais 100%, c'est toujours sous réserve que la théorie, que l'on utilise, n'est pas contradictoire, ce qui pour AP (arithmétique de Peano) est impossible à prouver.

[aviateur]

@arbre Je ne comprends toujours rien à tes explications et à ton jargon pseudo-scientifique.

[pascal16]

Programme en c#.
j'ai pris les 650 premières décimales de pi
j'ai décalé la virgule et l'ai mis dans un biginteger
j'ai multiplié par 2, j'ai ainsi l'équivalent de 2pi avec 650 décimales
je calcul 2^2017 et lui rajoute quinze 0 pour qu'il soit un entier en gardant 15-5=10 décimales lors des calculs.
je retranche autant de fois que possible 2pi*10^650
puis je divise par 10, je recommence
au final, je dois avoir la congruence modulo 2pi de 2^2017 avec 10 décimales
j'ai fait dans les 2814 soustractions (j'ai rajouté un compteur), ce qui m'enlève 4 à 5 décimales

Ci joint le programme avec "15" décimales.

Code: Tout sélectionner

{
            int n=0;
            BigInteger a = BigInteger.Parse("314159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872");
            a =BigInteger.Multiply(a, 2);
            // a contient les 618 décimales de 2pi
            BigInteger b = BigInteger.Pow(2, 2017);
            b = BigInteger.Multiply(b, 1000000000000000);
            BigInteger c;
            // b contient 2^2017 plus dix zeros pour à la fin revenir à 10 ch après la virgule

            while (BigInteger.Compare(b, 10000000000000000) >= 0)
            {
                c = BigInteger.Subtract(b, a);
                while (BigInteger.Compare(c, 0) >= 0)
                {
                    b = c;
                    c = BigInteger.Subtract(b, a);
                    n = n + 1;
                }
                a = BigInteger.Divide(a, 10);
            }

            textBox1.Text = b.ToString("N");
            textBox2.Text = n.ToString();
        }

[pascal16]

je sais que j'ai une erreur dans la condition d’arrêt car ça doit finir avec 2pi/10 et pas 2pi

C'est bien ça, j'ai sin(2^2017)=sin(5.632130)=-0.6061 maintenant

si tu veux 10 décimales de plus, pas de problème, le calcul se fait en 1 sec (visual c#).

[aviateur]

Bonjour
@pascal
Est ce que tu peux me donner la valeur de n? C'est à dire le nombre d'itérations.

D'autre part dans ton programme, essentiellement tu fais la différence de 2 entiers de grande taille (650 chiffres environ). Peux tu estimer le temps que met ta machine pour faire une seule opération de ce genre?
Merci d'avance

[pascal16]

j'ai 2806 boucles où j'effectue une soustraction utile
temps : 0.014 seconde pour le programme total sur un proc à 1.8Ghz

[Arbre]

Bonjour,

@Pascal : bravo.
1/Comment fais-tu pour calculer pi avec cette précision ?
2/Avec une précision de 10^{-10} tu obtiens combien ?

Cordialement.

[aviateur]

Rebonjour @pascal. J'essaie de comprendre ton programme, n'étant pas familier avec le langage que tu utilises. En effet je ne suis pas sûr d'avoir compris:
tu as et
Ensuite tu as 2 boucles imbriqués. Dans une première étape du retire successivement le nombre entier a au nombre b (avec un compteur nommé n) et tu arrêtes quand c=b-na devient négatif (je pense avoir compris cela). Dans ce cas n vaut approximativement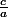 , c'est à dire ce qui est énorme. C'est là que je ne comprends. Il y a quelque chose qui m'échappe
Si tu pouvais expliquer ton algorithme cela serait bien pour valider ton résultat.

[Arbre]

J'ai récupérer les 1000 premières décimales de Pi et j'ai fait le calcul avec les 697, j'obtiens le même résultat qu'avec l'autre méthode, mais effectivement c'est beaucoup plus rapide.

Comment j'ai procédé :

1/J'ai calculer les sin(1) et cos(1) à l'aide des séries altèrnés qui les définies, les séries alternés m'assurent d'avoir le précision voulue et il suffit des 60 premiers termes soient une précision de 1/120!, un peu plus que ce qu'il faut.

2/J'ai calculer avec des integers en utilisant la formule d'addition d'un point du cercle (formule d'Euler), pour obtenir ce que souhaité.

[Arbre]

Salut,

Je mets ici les énoncés non encore résolu :

6 : critère de permutabilité
7 : détente permutative tombé par Pascal
11 : Partie convexe
13 : De l'arithmétique 3
15 : Un ensemble difficile à compter
16 : Le bijou convexe
18 : Plaindrome bien parenthésé tombé par Pascal
19 : fonction sinus compatible tombé par Pascal
20 : une question de rapidité
22 : multiplication ultra-rapide
23,24 : fonctions holderiennes
26 : la convexitude
29 : équation diophatienne
30 : arithmétiquement votre
37 : partie fractionnaire
38 : Catalan +1
39 : the inégalité tombé par Pascal
40 : the inégalité + tombé par Zyg
41 : valeur d'adhérence tombé par aviateur en utilisant la triche

Bonne journée.