Facile et simple ne sont pas confondus

[pascal16]

Aviateur.
la classe biginteger ne permet que des calculs sur des entiers, avec des résultats entiers (merci Arbre de m'en avoir parlé, car par défaut, le lien est pas fait dans visual studio).

le but : enlever autant de fois que possible 2pi à 2^2017
mais avec des entiers et 608 chiffres au minimum ( + 15 chiffres pour la précision finale)

idée sans se soucier pour l'instant des 15 chiffres
2*pi*10^608 est entier connu car certains ont calculé les 100000.... décimales de pi
c'est aussi un multiple de 2pi avec 608 chiffres de précision
j'enlève autant de fois que possible 2*pi*10^608 à 2^2017
je divise 2*pi*10^608 par 10, il vaut alors 2*pi*10^607
j'enlève autant de fois que possible 2*pi*10^607 à ce qu'il reste, au passage, le chiffre de départ a lui aussi perdu 1 chiffre et la précision est toujours de l'ordre de l'entier.
je continue jusqu'à enlever 2*pi*10^0 et j'ai mon modulo

il y a 608 boucles, à chaque fois il y a en moyenne 5 soustractions (en gros il faut en 0 et 10 soustractions pour diminuer d'un chiffre) soit dans les 3040 soustractions utiles.
le 3000 boucles apportent donc des erreurs d'arrondis, vers 4-5 chiffres significatifs en moins

en multipliant par 10^15 au départ et en divisant par 10^15 à la fin, on récupère 15 chiffres après la virgule avec les 5 derniers erronés par les calculs

[Arbre]

énoncé 38 : Catalan +1
Résoudre .

[Arbre]

Salut,

énoncé 39 : the inégalité
A-t-on, ?

éditer suite à la remarque de Pascal

Bonne soirée.

[aviateur]

@arbre avec a et b proches de 1/2 tu ne pense pas que la réponse est triviale?

[Arbre]

Bonjour,

Pourquoi donc ?
Mais il est sûr qu'une fois une solution trouvée, le problème devient trivial.

[pascal16]

ln(1-a)+ln(1-b)=ln(1-a-b+ab)
et ln n'est-elle pas croissante ?
Ce qui donne plutôt l'inégalité dans l'autre sens

[Arbre]

Bravo, oui tu as raison.

[Arbre]

énoncé 40 : the inégalité +
A-t-on,

[pascal16]

je dirais un départ avec la tangente en 0 : y=x+1
puis une convexité pour dire que la pente de la tangente au point d'abscisse a >0 est toujours >1

[Arbre]

Il faudrait que tu rédiges plus (pour que je vois si cela marche), en effet je n'ai pas la même approche que toi.

[pascal16]

retour sur sin(2^2107)
ma seconde version se passe de la connaissance de pi (qui peut être calculé à part)
je calcule cos(2^2017) qui me donne au signe près sin (2^2017).
principe :
par le DL en 0 de cos(x), je calcule cos(1). On pourrait faire une étude de convergence, mais comme on peut pousser les calculs bien plus loin que ce que l'on veut, j'ai donc décidé de faire la méthode de la "perturbation", ce que Arbre fait en modifiant un peu les derniers chiffres et regarde si le résultat varie


partie 1, calcule de cos(1)
Comme la somme est alternée et décroissante en valeur absolue, j'utilise 1/fact(n) comme référence de précision. Tous les chiffres sont ici multipliés par 10^620, 620 étant le nombre de chiffres de précision du calcul. Pour simplifier l'algo un peu lourd avec des biginteger, je fais 2 calculs par boucle

au final je récupère cos(1) avec 620 chiffres significatifs

Code: Tout sélectionner

BigInteger cos1, fact, dln, prec;
            int n;
            int precision = 620;
            prec = BigInteger.Pow(10, precision);
            cos1 = prec;
            n = 3;
            fact = 2;
            dln = BigInteger.Divide(prec, fact);
            while ((BigInteger.Compare(dln, 1)) >= 1)
            {
                dln = BigInteger.Divide(prec, fact);
                cos1 = BigInteger.Subtract(cos1, dln);
               
                               
                fact = BigInteger.Multiply(fact, n * (n + 1));
                n = n + 2;
                dln = BigInteger.Divide(prec, fact);
                cos1=BigInteger.Add(cos1, dln);
               
                fact = BigInteger.Multiply(fact, n * (n + 1));
                n = n + 2;
            }
            textBox2.Text = cos1.ToString();
            textBox2.Refresh();

[pascal16]

Partie 2, facile en apparence

soit la relation
si U_1=cos(1), j'ai U_2=cos(2^1)..... et U_2017=cos(2^2017)

Comme pour le précédent calcul, tout est multiplié par 10^620.
Je réutilise les variables inutiles, "fact" me sert de"Un".
A la première écriture, si U vaut 10^620, U² est de l'ordre de 10^1240 puis 10^2480 à la boucle suivante, et ça explosait tout
J'ai réfléchi, et un simple décalage de virgule en divisant pas 10^620 va très bien
on peut même afficher cos(2^n) si on veut.
Le formatage final doit en théorie tenir compte d'une chose.
S'il y a 620 chiffres, cos()=0,les 620 chiffres
S'il y a 617 chiffres, cos()=0,000 les 617 chiffres
et ne pas oublier le chiffre devant

Code: Tout sélectionner

for (n=1;n<=2017; n++)
            {
                // calcul de U<- 2U²-1 pour avoir cos(x) <- cos(2x)
                // tous les chiffres sont multipliés par 10^650
                fact = BigInteger.Pow(fact, 2); //U²
                fact = BigInteger.Divide(fact, BigInteger.Pow(10, precision));
                // rétablissement de la bonne position de la virgule
                fact = BigInteger.Multiply(fact, 2);//2U²
                fact = BigInteger.Subtract(fact, BigInteger.Pow(10, precision));//2U²-1

            }

            textBox1.Text = fact.ToString();

[pascal16]

Conclusion
Avec mon premier calcul 2^2017 congrue à 5.632130 modulo 2pi
cos(2^2017 ) aprox cos( 5.632130)=0.7954444....

avec le calcul en précision=620, j'ai "7954447822507xxx" comme chiffres soit
cos(2^2017 )=0.7954447822507xxx
si j'augmente la précision, je garde le même radical 0.7954447822507, le reste change.

Conclusion, avec les arrondis de calculs, 620 chiffres de précision donnent un résultat à 13 chiffres de précision.

Si on fait un calcul mathématique simplifié de l'erreur, on se dit qu'il faudrait pet-être plus de décimales. Si on rajoute le fait que les arrondis peuvent se faire une fois dans le mauvais sens, une fois dans le bon sens, on obtient un résultat qui statistiquement est proche de ce que je trouve. Donc, pour gagner du temps de calcul, la méthode d'Arbre de la "perturbation" est bonne.

PS : le calcul de cos(1) met 0.013sec
la suite pour calculer cos(2^2017) met 0.34 sec
On pourrait dans cette partie avoir un nombre de chiffres significatifs variables car ça ne sert à rien lors des derniers calculs d'avoir autant de chiffres, le temps de calcul n'étant pas linéairement lié au nombre de chiffres de précision (pour 1240chiffres, on passe à 1.33sec, pour 2480, on passe 5.33sec).

[Arbre]

Bonjour,

@Pascal : Bravo.

Bonne journée.

[pascal16]

Merci.
Le gros avantage de la première méthode (le modulo) c'est qu'elle est applicable à n'importe quel nombre.
Le seconde (puissance de 2), pourrait elle passer par une décomposition en puissances de 2, puis faire des sommes de cosinus (pas très sympa).
La partie calcul de cos(1) est elle aussi utilisable pour tout chiffre, avec une convergence ultra rapide pour les petits chiffres.

[Arbre]

On peut aussi calculer sin(2^{2017}) en utilisant les forumules d'additions de 2 points du cercle (formule d'Euler).

[aviateur]

@pascal 16. J'ai regardé ta façon de trouver avec ton algorithme. Je pense que tu as trouvé la solution. Le temps de calcul est court et le système est numériquement stable. Encore faut il vérifier que la solution donnée correspond à la précision demandée. Ici c'est le cas, j'ai bien sûr vérifié cela.
Par contre l'autre méthode ("la partie de calcul de cos(1)") où je pense que tu calcules par itérations ne peut pas donner la solution. En effet la méthode est complètement instable et cela se voit très bien: Puisque , une petite numérique sur 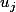donne


Comme on voit que l'erreur pour le calcul de est de l'ordre de
.

Autrement dit une petite approximation de \epsilon sur le calcul de cos(1) va donner une erreur de l'ordre de
pour le calcul de
Avec cela donne une "précision" de

Même avec j=18 on trouve une amplification d'erreur (ce qui est beaucoup lorsqu'on cherche un nombre entre -1 et1 !!!

[Arbre]

Non, j'ai fait le calcul par les 2 méthodes (avec l'approximation de Pi et aussi calcul avec la formule d'Euler) ont trouve la même chose, bon bref je m'étais fait la même remarque, mais pourtant cela donne la bonne solution, fais le calcul si tu ne me crois pas (les |u_j| sont en moyennes de la taille 1/2, ceci expliquerais cela)

[aviateur]

Non, j'ai fait le calcul par les 2 méthodes (avec l'approximation de Pi et aussi calcul avec la formule d'Euler) ont trouve la même chose, bon bref je m'étais fait la même remarque, mais pourtant cela donne la bonne solution, fais le calcul si tu ne me crois pas (les |u_j| sont en moyennes de la taille 1/2, ceci expliquerais cela)[*]

@ arbre tu es toujours incompréhensible.
.

[Arbre]

Si je ne faisais pas preuve de bonne volonté tu serais tout autant voir plus incompréhensible que ce que tu prétends pour moi.