Un exo débile et rigolo

[El_Gato]

Voilà un problème qui a une solution rigolote:

On se place dans le plan, plus précisemment dans , et on considère les rectangles dont les côtés sont bornés. On introduit la propriété (A) sur ces rectangles:

(A) au moins un des côtés du rectangle a une longueur entière.

On se donne un rectangle R, réunion disjointe d'un nombre fini de rectangles ayant la propriété (A).

Montrer que R a la propriété (A).

[yos]

Bonjour.
On considère un rectangle pavé avec des A-rectangles. Dés que deux d'entre eux ont un côté commun, on supprime cette frontière et on obtient un nouveau A-rectangle (plus grand) à la place. On arrive ainsi à un pavage sans que deux rectangles aient jamais un côté en commun. L'idéal serait de prouver que cela n'est pas faisable en dehors du cas trivial où le pavage se réduit à un rectangle (qui serait donc un A-rectangle). Hélas cela ne va pas. Mais je suis convaincu qu'en affinant l'idée, on arriverait au résultat.

[El_Gato]

Bonjour à tous,

Cet exo possède au moins deux solutions:

1- Une solution niveau Olympiades
2- Une solution niveau Olympiades + 1 année

1- Solution niveau Olympiades
Suivre le chemin dégagé par yos dans son post, en utilisant un argument de minimalité.

2- Solution niveau Olympiades + 1 année

Indication: un intervalle a une longueur entière si et seulement si:
.

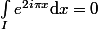
[Alpha]

Bonjour,

hier, en utilisant les intégrales doubles en maths, nous avons démontré cette proposition en 5 lignes! Notre prof, qui rédige assez souvent des articles dans la RMS (Revue de la Filière Mathématiques), nous a dit que dans le prochain numéro de la RMS, une preuve exclusivement combinatoire de ce fait serait donnée, mais qu'elle prend bien 4-5 pages.

D'ailleurs voici la page internet correspondante :

http://www.rms-math.com/article.php3?id_article=844

Si vous le souhaitez, je pourrai, quand j'en aurai le temps, rédiger la preuve que nous avons vue en cours.

Alpha+

[El_Gato]

hier, en utilisant les intégrales doubles en maths, nous avons démontré cette proposition en 5 lignes!

Voir l'indication donnée ci-dessus avec les exponentielles. Effectivement cela prend deux-trois lignes.

une preuve exclusivement combinatoire de ce fait serait donnée, mais qu'elle prend bien 4-5 pages.

Il existe sûrement une preuve combinatoire comme celle que tu décris. Mais une autre preuve, correspondant à la solution 1 ci-dessus est beaucoup plus courte.

Elle utilise un argument de minimalité. Environ 12 lignes en tout.

[Alpha]

Dans le lien que j'ai envoyé, se trouvent à la fois la démo avec les intégrales doubles et celle combinatoire dont j'ai parlé.

A+