Exo arithmetique
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Mar 2008, 14:12
par aviateurpilot » 16 Mar 2008, 14:12
salut les amis, ca fait logtemps que j'ai pa posté un exo sur ce forum.
voila un,
soit
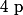
un premier
soit la suite
_{n\in\mathbb{N}}\in\mathbb{N}^{\mathbb{N}})
tel que
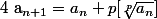
montrer que
=+\infty)
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Mar 2008, 15:03
par ThSQ » 16 Mar 2008, 15:03
grosse c*nerie
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Mar 2008, 16:39
par aviateurpilot » 16 Mar 2008, 16:39
ThSQ a écrit:Je dois pas comprendre car si a_1 = 0 c'est faux et si a_1 > 0, a_n est à valeurs entières et strictement croissante donc c'est évident. :help: :mur: :marteau:
si
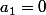
alors
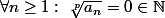
donc le resultat est vrai :id: !!
et le fait que

soit strictement croissante n'a pas de relation avec la solution


.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 16 Mar 2008, 16:52
par ThSQ » 16 Mar 2008, 16:52
Oulala, j'avais mal lu .....
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Mar 2008, 17:24
par Imod » 16 Mar 2008, 17:24
Les crochets désignent la partie entière , I presume ?
Imod
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Mar 2008, 17:40
par aviateurpilot » 16 Mar 2008, 17:40
Imod a écrit:Les crochets désignent la partie entière , I presume ?
Imod
oui :happy2:
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 16 Mar 2008, 17:53
par Imod » 16 Mar 2008, 17:53
Une remarque bête , il suffit de montrer qu'il existe
un indice pour lequel

est une puissance pième d'un entier .
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 16 Mar 2008, 18:22
par lapras » 16 Mar 2008, 18:22
Exact Imod :we:
Reste a la trouver :happy2:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Mar 2008, 19:32
par aviateurpilot » 16 Mar 2008, 19:32
Imod a écrit:Une remarque bête , il suffit de montrer qu'il existe
un indice pour lequel

est une puissance pième d'un entier .
Imod
oui bien sur,
voila le demo de ce que tu vien de dire.
ca si pour
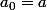
qui n soi pa une puissance p eme
\in\mathbb{N})
tel que
}=b^{p})
alors
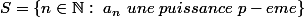
est infini. (demo par absurde).
si
)
alors
\in S)
et
>h)
(absurde).
mais le probleme principal ici c'est monter que
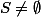
:++:.
(dans ma demo j'ai modeliser le probleme avec des couple de
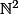
)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 16 Mar 2008, 19:44
par lapras » 16 Mar 2008, 19:44
salut
que veut dire p(a) ?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Mar 2008, 19:54
par aviateurpilot » 16 Mar 2008, 19:54
lapras a écrit:salut
que veut dire p(a) ?
ce que je vien de dire c'est pa la solution, mais il monter cette implication
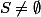
===>
=+\infty)
j'ai supposer qu'on a construit pour
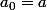
quelconque dans N.
un undice que j'ai nommer
)
tel que
})
puissance p-eme.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 19 Mar 2008, 22:10
par aviateurpilot » 19 Mar 2008, 22:10
N.B: je posterai ma solution apres demain
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 20 Mar 2008, 07:07
par lapras » 20 Mar 2008, 07:07
salut aziz
Peux tu nous laisser un délai jusqu'à ce week end ? car pesonnellement (et ca peut etre valable pour d'autres) je n'ai pas trop le temps de chercher.
:++:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Mar 2008, 10:05
par aviateurpilot » 20 Mar 2008, 10:05
lapras a écrit:salut aziz
Peux tu nous laisser un délai jusqu'à ce week end ? car pesonnellement (et ca peut etre valable pour d'autres) je n'ai pas trop le temps de chercher.
:++:
ok :++:, apres 7j alors
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 26 Mar 2008, 22:47
par Imod » 26 Mar 2008, 22:47
aviateurpilot a écrit:ok :++:, apres 7j alors
Je crois que tu peux donner ta solution ou au moins un indice , personnellement je suis sec :hum:
Imod
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 27 Mar 2008, 08:34
par lapras » 27 Mar 2008, 08:34
Oui du moment qu'on a pas a0 ca semble difficile...
En plus ca fait longtemps que j'ai pas vu de démos d'arithmétiques d'aviateur pilote, elles sont si élégantes !
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Mar 2008, 21:11
par aviateurpilot » 27 Mar 2008, 21:11
Imod a écrit:Je crois que tu peux donner ta solution ou au moins un indice , personnellement je suis sec :hum:
Imod
ok,
1)
^p-h^p\equiv 1[ph])
2) on peux utiliser a la place de la suite a_n
la suite
)
tel que :
i)
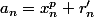
ii)
^{p}-x_n^p\})
iii)
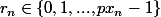
iiii)
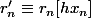
et etudie

et
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
est une puissance pième d'un entier .