Un exercice d'olympiad
Olympiades mathématiques, énigmes et défis
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 23 Oct 2010, 21:47
par jack01 » 23 Oct 2010, 21:47
bonjour;
Montrer que pour n entier, il existe un entier m tel que :
-1)^n=sqrt(m)-sqrt(m-1))
je m'excuse de mon permiere discussion :mur:
NB:je veux mette la correction après 5 de votre réponse :ptdr:
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 24 Oct 2010, 08:40
par nodjim » 24 Oct 2010, 08:40
As tu fait quelques essais ?

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 24 Oct 2010, 11:25
par Olympus » 24 Oct 2010, 11:25
Salut !
On peut commencer par prouver que pour tout

il existe deux entiers naturels

tels que
^n = x_n +\sqrt{2}y_n)
et
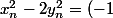^n)
. Ensuite on conclut en distinguant les cas où

est pair, et impair .
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 24 Oct 2010, 15:02
par jack01 » 24 Oct 2010, 15:02
nodjim a écrit:As tu fait quelques essais ?
j'ai la solution que je le fais moi meme :ptdr:
et pour Olympus la solution et tres proche ne demande pas de

-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 24 Oct 2010, 19:14
par jack01 » 24 Oct 2010, 19:14
pas de reponse :cry:
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 24 Oct 2010, 19:28
par nodjim » 24 Oct 2010, 19:28
Euh, tu veux quelque chose ? J'ai cru comprendre que tu avais résolu...
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 24 Oct 2010, 19:50
par jack01 » 24 Oct 2010, 19:50
est ce que tu la resoulut
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 25 Oct 2010, 08:14
par nodjim » 25 Oct 2010, 08:14
Ma solution, qui tient du raisonnement par récurrence:
C'est assez vite qu'on se rend compte comment on passe de (aV2-b)=(V2-1)^n à (a'V2-b)= (V2-1)^(n+1):
a'=-(a+b)
b'=-(2a+b)
On compare les carrés des termes aV2 et b qui sont 2a² et b². Si la différence est + ou -1, par récurrence, on montre que c'est vrai aussi pour 2a'²-b'².
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 25 Oct 2010, 18:21
par jack01 » 25 Oct 2010, 18:21
oh nodjim la solution ne demande pas de sa; c'est tres proche.
NB:il rest 1 reponse pour voire la sotion

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Oct 2010, 18:31
par Ben314 » 25 Oct 2010, 18:31
jack01 a écrit:oh nodjim la solution ne demande pas de sa; c'est tres proche.
NB:il rest 1 reponse pour voire la sotion
Je comprend pas trop ce que tu veut comme réponse : ça fait déjà deux solutions (justes) que l'on te propose...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 25 Oct 2010, 18:40
par Jimm15 » 25 Oct 2010, 18:40
Bonsoir,
En fait, je crois quil voulait vous faire chercher des pistes voire des réponses et quau bout de la cinquième mauvaise réponse, vous donner la solution...

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 25 Oct 2010, 18:41
par Olympus » 25 Oct 2010, 18:41
jack01 a écrit:et pour Olympus la solution et tres proche ne demande pas de

Direction poubelle pour ma solution donc ?
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 25 Oct 2010, 18:58
par jack01 » 25 Oct 2010, 18:58
bismi llah
solution du l'exercice
EX
Montrer que pour n entier, il existe un entier m tel que :
-1)^n=sqrt(m)-sqrt(m-1))
reponse
on a
-1)^n=sqrt(m)-sqrt(m-1))
-----(1)
en inverse on obtient :
-1})^n=\frac{1}{sqrt(m)-sqrt(m-1)})
en multiplient par la conjugue on obtient
+1)^n=sqrt(m)+sqrt(m-1))
---------(2)
donc on a un system en aditionnant (1) et (2)
on obtient
=(sqrt(2)-1)^n+(sqrt(2)+1)^n)
implique
-1)^n+(sqrt(2)+1)^n)^2)
donc m est un entier
merci de vorte passage :lol3:
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 25 Oct 2010, 19:00
par windows7 » 25 Oct 2010, 19:00
t'es cinglé toi.
et apprend le latex tu serais gentil fiston.
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 25 Oct 2010, 19:02
par jack01 » 25 Oct 2010, 19:02
comment va menant
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 25 Oct 2010, 19:22
par windows7 » 25 Oct 2010, 19:22
bon enfait ya plus urgent que le latex, faut apprendre le francais
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 25 Oct 2010, 19:24
par jack01 » 25 Oct 2010, 19:24
windows7 a écrit:bon enfait ya plus urgent que le latex, faut apprendre le francais
pour le francai ; le probleme vient du clavie :triste:
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 25 Oct 2010, 19:55
par nodjim » 25 Oct 2010, 19:55
Jack01,
A un problème donné, il y a parfois plusieurs solutions possibles. Ici, on en dénombre déja 3, peut être en existe t il d'autres. Si tu poses une question dont tu connais déja une solution, que tu as résolue seul où par une lecture quelconque, admets qu'il existe d'autres solutions et analyse les, ça ne pourra que t'être utile. Il est d'usage sur ce site de ne pas rédiger l'intégralité d'une démonstration, on suppose que les lecteurs avisés complètent les trous. Si la démo est fausse, ne te fais pas de soucis, c'est souvent très vite découvert.
Cela dit, bienvenue à toi sur ce site.
-
jack01
- Membre Naturel
- Messages: 56
- Enregistré le: 22 Oct 2010, 21:57
-
 par jack01 » 27 Oct 2010, 14:28
par jack01 » 27 Oct 2010, 14:28
nodjim a écrit:Jack01,
A un problème donné, il y a parfois plusieurs solutions possibles. Ici, on en dénombre déja 3, peut être en existe t il d'autres. Si tu poses une question dont tu connais déja une solution, que tu as résolue seul où par une lecture quelconque, admets qu'il existe d'autres solutions et analyse les, ça ne pourra que t'être utile. Il est d'usage sur ce site de ne pas rédiger l'intégralité d'une démonstration, on suppose que les lecteurs avisés complètent les trous. Si la démo est fausse, ne te fais pas de soucis, c'est souvent très vite découvert.
Cela dit, bienvenue à toi sur ce site.
merci ; mon quetion c'etait pour vous;de refrechire de augmenter vos connessance en math :zen:
et merci encore de ton passage
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités