Espace euclidien

par **Timothé Lefebvre** » 23 Nov 2009, 18:37

Bonsoir

Une OIM sympathique, pas très dure et généralisable !

Soit

un ensemble fini formé de points de coordonnées entières dans l'espace euclidien et soient

,

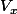
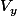
et

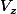
les ensembles formés des projections de

sur les plans

,

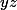
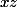
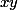
respectivement.
Démontrer que :

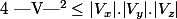
où |A| désigne le nombre d'éléments de l'ensemble fini A.

Bonne soirée

par **ffpower** » 24 Nov 2009, 01:21

Je suis pas sur d avoir compris. Si on prend pour V les sommets d un cube, V aura 16 points,et chaque projection aura 4 points. Or 16² n est pas inferieur a 4*4*4

par **Ben314** » 24 Nov 2009, 12:07

Un cube à 16 sommets, joli cube !!!

par **Timothé Lefebvre** » 24 Nov 2009, 16:05

Salut

Je vais reformuler l'énoncé.

L'espace est rapporté à un repère orthonormé (Oxyz) et V est un ensemble fini de points de cet espace. On désigne respectivement par Vx, Vy et Vz les ensembles constitués par les projections orthogonales des points de V sur les trois plans (Oyz), (Ozx) et (Oxy).

Mq

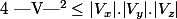
où |A| est le cardinal de l'ensemble fini A.

par **laquestion** » 24 Nov 2009, 23:45

on peut sans perdre de generalité considérer que si (x,y,z) sont les coordonnées d'un point, il existe un point de coordonnée d'absysse x-1 , un point d'ordonnée y-1 et un point de cote z-1...

par **Timothé Lefebvre** » 25 Nov 2009, 06:51

J'ai utilisé une récurrence puis C-S pour conclure.

par **Ben314** » 25 Nov 2009, 14:55

Il n'y a besoin ni de récurrence, ni de Cauchy-Schwart !!!!
Mais seulement que, si on a n possibilitées pour a et m pour b, alors il y a nm possibilitées pour le couple (a,b) !!

par **Timothé Lefebvre** » 25 Nov 2009, 15:15

Je ne pense pas que ce soit aussi simple ...

par **laquestion** » 25 Nov 2009, 17:31

en s'arrageant comme je l'ai dit plus haut pour que toutes abscisses soit couvertes jusqu'à X, les ordonnees jusqu'a Y et les cotes jusqu'à Z
on a bien V^2<(XYZ)^2=ZY.ZX.XY=Vx.Vy.Vz

Espace euclidien

Espace euclidien

Qui est en ligne