Bonjour,
Je cherche à déterminer les valeurs de x, y et z sachant que ce sont trois entiers naturels.
J'ai les équations suivantes (je n'ai pas réussi à utiliser l'éditeur d'équation donc je mets les équations de manière "brute".)
x+y+z=14
x^2+y^2+z=76
y^2+z^2+x=36
x^2+z^2+y=58
En testant toutes les possibilités (pour x, y et z de 0 à 14), la seule solution est (7; 5; 2) (soit x=7, y=5, z=2).
Toutefois, je n'ai pas trouvé comment démontrer cette solution.
J'ai essayé de remplacer x (ou y ou z) par 14-y-z dans une des équations et de combiner les équations, mais je ne suis pas parvenu à isoler une des trois inconnues (je me retrouve avec du y*z...)
Pourriez-vous m'aider ?
Cordialement,
EMan.
Equations du second degré à trois inconnues
7 messages
- Page 1 sur 1
Re: Equations du second degré à trois inconnues
Salut,
Pour avoir une réponse adaptée, il faudrait que tu nous précises à quel niveau d'étude tu es.
Pour avoir une réponse adaptée, il faudrait que tu nous précises à quel niveau d'étude tu es.
Re: Equations du second degré à trois inconnues
Je suis en terminale S (ma question ne concerne pas un devoir scolaire, je me demandais simplement comment résoudre ces équations).
Re: Equations du second degré à trois inconnues
Salut,
Par exemple ainsi (sans besoin de connaissances particulières) :
x+y+z=14
x^2+y^2+z=76
y^2+z^2+x=36
x^2+z^2+y=58
x = 14-y-z
(14-y-z)^2+y^2+z=76
y^2+z^2+14-y-z=36
(14-y-z)^2+z^2+y=58
196+y²+z²-28y-28z+2yz+y^2+z=76
y^2+z^2+14-y-z=36
196+y²+z²-28y-28z+2yz+z^2+y=58
196+2y²+z²-28y-28z+2yz+z=76 (1)
y^2+z^2+14-y-z=36 (2)
196+y²+2z²-28y-28z+2yz+y=58 (3)
(1) - (3) -->
y²-z²+z-y=18 (4)
y²+z²+14-y-z=36 (2)
(4) - (2) --->
-2z²-14+2z=-18
2z²-2z-4 = 0
z²-z-2 = 0 --> z = 2
dans(4) --> y² - 4 + 2 - y = 18
y² - y - 20 = 0 --> y = 5
et x = 14-y-z = 14 - 2 - 5 = 7

Par exemple ainsi (sans besoin de connaissances particulières) :
x+y+z=14
x^2+y^2+z=76
y^2+z^2+x=36
x^2+z^2+y=58
x = 14-y-z
(14-y-z)^2+y^2+z=76
y^2+z^2+14-y-z=36
(14-y-z)^2+z^2+y=58
196+y²+z²-28y-28z+2yz+y^2+z=76
y^2+z^2+14-y-z=36
196+y²+z²-28y-28z+2yz+z^2+y=58
196+2y²+z²-28y-28z+2yz+z=76 (1)
y^2+z^2+14-y-z=36 (2)
196+y²+2z²-28y-28z+2yz+y=58 (3)
(1) - (3) -->
y²-z²+z-y=18 (4)
y²+z²+14-y-z=36 (2)
(4) - (2) --->
-2z²-14+2z=-18
2z²-2z-4 = 0
z²-z-2 = 0 --> z = 2
dans(4) --> y² - 4 + 2 - y = 18
y² - y - 20 = 0 --> y = 5
et x = 14-y-z = 14 - 2 - 5 = 7
Re: Equations du second degré à trois inconnues
Merci beaucoup, c'est que je voulais.
J'étais sur la bonne voie mais je m'étais arrêté trop tôt dans le raisonnement.
J'étais sur la bonne voie mais je m'étais arrêté trop tôt dans le raisonnement.
Re: Equations du second degré à trois inconnues
Salut,
Si tu fait l'équation (4) moins la (3) [pour virer les ] tu obtient
] tu obtient  qui se factorise gentiment en
qui se factorise gentiment en (x\!+\!y\!-\!1)\!=\!22) ce qui, vu les diviseur de 22 et le fait que
ce qui, vu les diviseur de 22 et le fait que  laisse peu de choix :
laisse peu de choix :
- Soit et
et 
- Soit et
et 
Vu que tu cherche des solutions entières positives, a mon sens, tu peut aussi essayer d'utiliser les "outil classiques" de l’arithmétique, plus précisément la notion de divisibilité :EMan a écrit:
Si tu fait l'équation (4) moins la (3) [pour virer les
- Soit
- Soit
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Equations du second degré à trois inconnues
une autre méthode:

on additionne les trois dernières égalités du système:
+x+y+z=170)
+14=170)

la deuxième égalité donne
=76)
=2=2 \times 1)
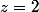
la troisième égalité donne:
=36)
=42=7 \times 6)
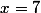
la quatrième égalité donne:
=58)
=20=5 \times 4)
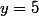
on additionne les trois dernières égalités du système:
la deuxième égalité donne
la troisième égalité donne:
la quatrième égalité donne:
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
