Equations du second degré
Olympiades mathématiques, énigmes et défis
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 09 Oct 2008, 20:15
par Mhdi » 09 Oct 2008, 20:15
Salut,
Après je ne sais combien de temps, je peux enfin me connecter, et je vous vient avec un exercice. :we:
Soient:
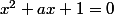
ayant les solutions m et n
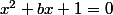
ayant les solutions m' et n'
Calculer "p" en fonction de a et de b:
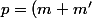(n+n')(m-m')(n-n'))
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 09 Oct 2008, 20:27
par Zweig » 09 Oct 2008, 20:27
-
Mhdi
- Membre Relatif
- Messages: 126
- Enregistré le: 26 Avr 2008, 14:09
-
 par Mhdi » 10 Oct 2008, 00:10
par Mhdi » 10 Oct 2008, 00:10
Chapeau Zweig !
Allez, comme tu sembles en forme, voici un p'tit cadeau :
EX1:Soient

tels que :
 : |ax^2 + bx + c|\le 1)
1)MQ

2)MQ

3)MQ
 EX2:
EX2:MQ si

et

, on a :
 PS : MQ=Montrer que
PS : MQ=Montrer que
-
miikou
- Membre Rationnel
- Messages: 642
- Enregistré le: 07 Juil 2008, 18:38
-
 par miikou » 10 Oct 2008, 12:47
par miikou » 10 Oct 2008, 12:47
ex 1)
1)on prend x=0 |c| < 1
2)on prend x=1 |a+b+c|<1
x=-1 |a-b+c|<1
on a donc | (a+b+c)+(a-b+c)| < |a+b+c|+|a-b+c| < 1+1
soit encore 2|a+c| < 2 donc |a+c| < 1
3)question piège ??
si a et b non sont pas nuls alors en valeur absolue ax²+bx+c tend vers + infini
donc a et b sont nuls.
or |c| < 1 => c² < 5 donc a²+b²+c²<5
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 12 Oct 2008, 13:27
par lapras » 12 Oct 2008, 13:27
Ex 2 :
en élevant au carré l'expression c'est easy il me semble !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités