Équation fonctionnelle
Olympiades mathématiques, énigmes et défis
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 04 Mai 2014, 11:53
par Matt_01 » 04 Mai 2014, 11:53
Bonjour,
Existe-t-il une fonction f strictement croissante, définie de R dans R, telle que f'=fof ?
-
radoude
- Membre Naturel
- Messages: 87
- Enregistré le: 26 Avr 2014, 15:02
-
 par radoude » 04 Mai 2014, 14:43
par radoude » 04 Mai 2014, 14:43
Bonjour
L'énoncé signifie-t-il que dom f(x) =R et que Im f(x)=R?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Mai 2014, 14:50
par Sourire_banane » 04 Mai 2014, 14:50
Salut,
radoude a écrit:Bonjour
L'énoncé signifie-t-il que dom f(x) =R et que Im f(x)=R?
?
Qu'entends-tu par dom ? f est-elle forcément polynômiale ?
Oui, on restreint et on corestreint f à R.
-
radoude
- Membre Naturel
- Messages: 87
- Enregistré le: 26 Avr 2014, 15:02
-
 par radoude » 04 Mai 2014, 14:58
par radoude » 04 Mai 2014, 14:58
radoude a écrit:Bonjour
L'énoncé signifie-t-il que dom f(x) =R et que Im f(x)=R?
Si oui ("définie de R dans R") alors la réponses est non
En effet, il faut f'(x)=f(f(x))>=0 pour tout x.
Or f(x) "parcourt" tous les réels et donc f(f(x)) aussi.
f(f(x)) ne peut donc pas être positif ou nul pour tout x.
J'espère ne pas avoir raconté n'importe quoi.
-
radoude
- Membre Naturel
- Messages: 87
- Enregistré le: 26 Avr 2014, 15:02
-
 par radoude » 04 Mai 2014, 14:59
par radoude » 04 Mai 2014, 14:59
Sourire_banane a écrit:Salut,
?
Qu'entends-tu par dom ? f est-elle forcément polynômiale ?
Oui, on restreint et on corestreint f à R.
dom f(x) est le domaine de définition de f(x) et Im f(x) son domaine image
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Mai 2014, 15:01
par Sourire_banane » 04 Mai 2014, 15:01
radoude a écrit:dom f(x) est le domaine de fe définition de f(x) et Im f(x) son domaine image
Attention, dans ce cas on dira f plutôt que f(x). Cela n'a pas de sens de parler du domaine ou de l'image d'une expression. On pourra en parler dans le cas d'une fonction.
-
radoude
- Membre Naturel
- Messages: 87
- Enregistré le: 26 Avr 2014, 15:02
-
 par radoude » 04 Mai 2014, 15:07
par radoude » 04 Mai 2014, 15:07
ok c'est logique. Je repose en de bon termes: l'énoncé veut-il dire que dom f=R et que im f=R?
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Mai 2014, 15:09
par Sourire_banane » 04 Mai 2014, 15:09
radoude a écrit:Si oui ("définie de R dans R") alors la réponses est non
En effet, il faut f'(x)=f(f(x))>=0 pour tout x.
Or f(x) "parcourt" tous les réels et donc f(f(x)) aussi.
f(f(x)) ne peut donc pas être positif ou nul pour tout x.
J'espère ne pas avoir raconté n'importe quoi.
J'ai un doute. En fait dans la plupart des énoncés, on dit que f est de R dans R sans donner des indications précises sur la manière dont f décrit ces ensembles et si f n'est pas seulement restreinte à un intervalle plus petit. C'est le cas de exponentielle réelle que l'on dit souvent définie de R dans R alors qu'elle l'est véritablement de R dans R+*. Cela nous importe moins que dans le cas du logarithme par exemple, où cette fois-ci la donnée de l'ensemble de départ est primordiale pour que la fonction soit définie.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 04 Mai 2014, 15:09
par Matt_01 » 04 Mai 2014, 15:09
Ma notation (et de manière générale) signifie que l'image de f est inclus dans R.
Tel que tu le décris, la notion de surjectivité serait obsolète.
-
radoude
- Membre Naturel
- Messages: 87
- Enregistré le: 26 Avr 2014, 15:02
-
 par radoude » 04 Mai 2014, 15:12
par radoude » 04 Mai 2014, 15:12
ok alors ma démonstration ne tient pas
-
radoude
- Membre Naturel
- Messages: 87
- Enregistré le: 26 Avr 2014, 15:02
-
 par radoude » 04 Mai 2014, 15:29
par radoude » 04 Mai 2014, 15:29
Oui: f(x)=0 mais je suppose que ce n'est pas la réponse attendue.
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 04 Mai 2014, 15:30
par Sourire_banane » 04 Mai 2014, 15:30
radoude a écrit:Oui: f(x)=0 mais je suppose que ce n'est pas la réponse attendue.
Elle convient, reste à savoir si c'est la seule ou pas.
Edit : Non, c'est bon. On te demande s'il en existe une. Tu as exhibé une fonction qui marche, donc cela devrait suffire.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 04 Mai 2014, 15:37
par Matt_01 » 04 Mai 2014, 15:37
Bon, f non nulle, sinon ça n'a pas beaucoup d'intérêt.
Edit : je sais pas si ça revient au même, mais initialement c'est f strictement croissante.
-
Kelenner
- Messages: 9
- Enregistré le: 14 Juin 2013, 07:43
-
 par Kelenner » 05 Mai 2014, 16:41
par Kelenner » 05 Mai 2014, 16:41
Bonjour,
Je fais une tentative.
1) Comme

est strictement croissante, on a
\geq 0)
pour tout

, et
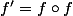
est strictement croissante. Si
)
s'annulait pour un

, elle serait strictement négative pour
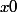
pour tout

.
2) La fonction
)
tend vers l'infini si

tend vers

.
En effet, soit

fixé et
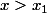
. On utilise le théorème des accroissements finis: il existe
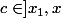
[ tel que
-f(x_1)=(x-x_1)f^{\prime}(c)\geq (x-x_1)f^{\prime}(x_1))
par croissance de
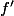
, et le résultat s'ensuit puisque
>0)
.
3) Comme
=f(f(x)))
, on a aussi
)
qui tend vers

.
4)
-x)
tend vers l'infini si

tend vers l'infini.
En effet, soit
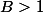
. On peut trouver
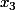
tel que
>B)
pour
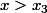
. Alors pour
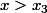
, il existe
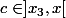
tel que:
=f(x_3)+(x-x_3)f^{\prime}(c)\geq f(x_3)+(x-x_3)B)
de sorte que
-x\geq f(x_3)+(B-1)x-x_3 B)
tend bien vers

si

tend vers

.
6) Il existe
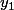
tel que
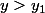
implique que
>y)
. Soit
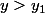
. On écrit que, pour
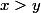
, il existe
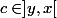
tel que
=f(y)+(x-y)f^{\prime}(c)\geq f(y)+(x-y)f^{\prime}(y))
On peut choisir
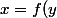)
puisque
>y)
, ce qui donne:
)\geq f(y)+(f(y)-y)f^{\prime}(y)=f(y)+(f(y)-y)f(f(y)))
Comme
-y)
tend vers

, le second membre est strictement plus grand que le premier pour

grand, contradiction.
7) Conclusion: une telle fonction n'existe pas.
Cordialement.
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 05 Mai 2014, 18:41
par Matt_01 » 05 Mai 2014, 18:41
J'avais une solution un peu similaire, qui consiste à montrer que x - f^(-1)(x) > 1 à partir d'un certain rang (en examinant la dérivée de cette fonction, qui tend vers 1 en l'infini).
A partir de ce rang, on a f(f(x)) > f(x) et donc
=f(y) + \int_y^x f(f(t))dt \geq f(y) + (x-max(f^{-1}(x),y)f(x))
et on fait tendre de chaque coté pour voir la contradiction.
-
Jul29
- Membre Naturel
- Messages: 40
- Enregistré le: 28 Oct 2009, 20:34
-
 par Jul29 » 04 Juin 2014, 21:18
par Jul29 » 04 Juin 2014, 21:18
Si f'(x)>0 cela n'implique pas que f tende vers l'infini.
Je ne sais pas si un tel f existe mais il semble facile de trouver f(x)=f'(f'(x))
-
Kelenner
- Messages: 9
- Enregistré le: 14 Juin 2013, 07:43
-
 par Kelenner » 05 Juin 2014, 05:47
par Kelenner » 05 Juin 2014, 05:47
Jul29 a écrit:Si f'(x)>0 cela n'implique pas que f tende vers l'infini.
Je ne sais pas si un tel f existe mais il semble facile de trouver f(x)=f'(f'(x))
Bonjour,
On a en plus que f' est strictement croissante, lire le point 2) de ma réponse.
Bien cordialement.
-
Jul29
- Membre Naturel
- Messages: 40
- Enregistré le: 28 Oct 2009, 20:34
-
 par Jul29 » 05 Juin 2014, 22:14
par Jul29 » 05 Juin 2014, 22:14
Kelenner a écrit:Bonjour,
On a en plus que f' est strictement croissante, lire le point 2) de ma réponse.
Bien cordialement.
bonsoir, en effet ce point m'a echappe.
Pourrait-on cependant imaginer que f ne soit definie que sur un intervalle ? Mais il me semble que la preuve est generalisable a ce cas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
 est strictement croissante, on a
est strictement croissante, on a \geq 0) pour tout
pour tout  , et
, et 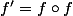 est strictement croissante. Si
est strictement croissante. Si ) s'annulait pour un
s'annulait pour un  , elle serait strictement négative pour
, elle serait strictement négative pour 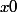 pour tout
pour tout  .
.) tend vers l'infini si
tend vers l'infini si  tend vers
tend vers  .
. fixé et
fixé et 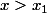 . On utilise le théorème des accroissements finis: il existe
. On utilise le théorème des accroissements finis: il existe 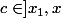 [ tel que
[ tel que-f(x_1)=(x-x_1)f^{\prime}(c)\geq (x-x_1)f^{\prime}(x_1))
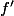 , et le résultat s'ensuit puisque
, et le résultat s'ensuit puisque >0) .
.=f(f(x))) , on a aussi
, on a aussi ) qui tend vers
qui tend vers  .
.-x) tend vers l'infini si
tend vers l'infini si  tend vers l'infini.
tend vers l'infini.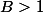 . On peut trouver
. On peut trouver 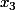 tel que
tel que >B) pour
pour 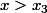 . Alors pour
. Alors pour 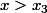 , il existe
, il existe 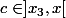 tel que:
tel que:=f(x_3)+(x-x_3)f^{\prime}(c)\geq f(x_3)+(x-x_3)B)
-x\geq f(x_3)+(B-1)x-x_3 B) tend bien vers
tend bien vers  si
si  tend vers
tend vers  .
.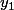 tel que
tel que 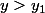 implique que
implique que >y) . Soit
. Soit 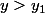 . On écrit que, pour
. On écrit que, pour 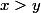 , il existe
, il existe 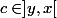 tel que
tel que=f(y)+(x-y)f^{\prime}(c)\geq f(y)+(x-y)f^{\prime}(y))
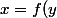) puisque
puisque >y) , ce qui donne:
, ce qui donne:)\geq f(y)+(f(y)-y)f^{\prime}(y)=f(y)+(f(y)-y)f(f(y)))
-y) tend vers
tend vers  , le second membre est strictement plus grand que le premier pour
, le second membre est strictement plus grand que le premier pour  grand, contradiction.
grand, contradiction.