Equation cubique
Olympiades mathématiques, énigmes et défis
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 14 Aoû 2008, 23:30
par lapras » 14 Aoû 2008, 23:30
Hi, nice equation, It seems difficult but it's not too much.
Solve the following eqation, with x,y integers > 1 :
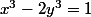
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 15 Aoû 2008, 06:35
par guigui51250 » 15 Aoû 2008, 06:35
lapras a écrit:Hi, nice equation, It seems difficult but it's not too much.
Solve the following eqation, with x,y integers > 1 :
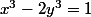
Hi, I think there is nothing solution, is it right?
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 15 Aoû 2008, 09:15
par nodgim » 15 Aoû 2008, 09:15
Bonjour.
On peut réécrire 2y^3=x^3-1
il faut x impair, x=2x+1
(2x+1)^3-1=8x^3+12x²+6x+1-1=2y^3
4x^3+6x²+3x=y^3
x(4x²+6x+3)=y^3
x(2x(2x+3)+3) est un cube ?
x fait obligatoirement partie des diviseurs de y. Mais hélas 2x(2x+3)+3 est à +3 modulo x. Pour 3, ça ne marche pas, c'était la seule possiblité.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 15 Aoû 2008, 09:25
par ThSQ » 15 Aoû 2008, 09:25
Classique, plus généralement résoudre :

en entiers relatifs
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 15 Aoû 2008, 10:10
par lapras » 15 Aoû 2008, 10:10
Nodgim > PGCD(x, x(2x+3) + 3) = 1 ou 3
dans le cas
a) PGCD(x, x(2x+3) + 3) = 1
alors xest un cube, et x divise y
tu dis que x(2x+3) + 3 divise aussi y, mais en quoi cela est il génant que x(2x+3) = 3 [mod x] ?
ThSQ > Merci pour l'équation :)
Mon équation cubique est elle vraiment un classique ?
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 15 Aoû 2008, 11:01
par guigui51250 » 15 Aoû 2008, 11:01
lapras a écrit:Mon équation cubique est elle vraiment un classique ?
bah c'est surtout un cas particulier de ton équation

je crois que c'est ça que tu as à résoudre pour ton stage.
me I have find nothing solution :happy2:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 15 Aoû 2008, 11:03
par lapras » 15 Aoû 2008, 11:03
Non l'équation que j'avais c'était

ce qui est beaucoup plus général, et il y a des solutions !
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 15 Aoû 2008, 11:09
par ThSQ » 15 Aoû 2008, 11:09
lapras a écrit:Mon équation cubique est elle vraiment un classique ?
La notion de classique est toute relative mais le cas général (x^3+y^3=2z^3) est vu souvent en même temps que x^3+y^3=z^3 (et est plus facile à résoudre).
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 15 Aoû 2008, 11:14
par lapras » 15 Aoû 2008, 11:14
Ah oui le cas n = 3 du théoreme de fermat.
Mais je suppose que dans ta solution tu utilise

et tu te places dans

pour ensuite utiliser la théorie qui est derrière ?
ce n'est pas un classique pour les olympiades je pense :happy2:
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 15 Aoû 2008, 16:55
par ThSQ » 15 Aoû 2008, 16:55
lapras a écrit:tu utilise

Ca se fait de façon 100% élémentaire aussi.
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 15 Aoû 2008, 19:03
par lapras » 15 Aoû 2008, 19:03
Oui car j'en ai une preuve élémentaire ! :we: (sinon je ne l'aurai pas posté)
Ceux qui veulent tenter sont les bienvenues...
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 28 Oct 2008, 20:03
par lapras » 28 Oct 2008, 20:03
Bonsoir,
alors, personne n'a de preuve élémentaire ?
Sinon, je poste ma solution...
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 28 Oct 2008, 20:25
par guigui51250 » 28 Oct 2008, 20:25
depuis le temps je pense qu'il vaudrait mieux que tu poste
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 28 Oct 2008, 20:54
par lapras » 28 Oct 2008, 20:54
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 28 Oct 2008, 21:02
par guigui51250 » 28 Oct 2008, 21:02
euh j'ai pas saisi ton histoire de PGCD, à vrai dire j'ai jamais étudié les PGCD... je vois ça à la rentrée :we:
Merci quand même pour ton explication, je la relirais dans quelques semaines
:we:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 29 Oct 2008, 00:27
par Imod » 29 Oct 2008, 00:27
guigui51250 a écrit:euh j'ai pas saisi ton histoire de PGCD, à vrai dire j'ai jamais étudié les PGCD... je vois ça à la rentrée :we:
On voit ça en 3ème avec l'algorithme d'Euclide depuis quelques années ( en France en tout cas ) :zen:
Imod
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 29 Oct 2008, 08:38
par guigui51250 » 29 Oct 2008, 08:38
Imod a écrit:On voit ça en 3ème avec l'algorithme d'Euclide depuis quelques années ( en France en tout cas ) :zen:
Imod
lol oui mais on approfondi ça en terminale spé maths...
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 29 Oct 2008, 18:00
par lapras » 29 Oct 2008, 18:00
Autre équation sympa :
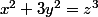
:we:
Bon courage
-
guigui51250
- Membre Complexe
- Messages: 2727
- Enregistré le: 30 Déc 2007, 11:00
-
 par guigui51250 » 31 Oct 2008, 19:09
par guigui51250 » 31 Oct 2008, 19:09
là j'avoue que je ne sais même pas par où commencer :mur: :mur:
:help:
-
Matt_01
- Habitué(e)
- Messages: 609
- Enregistré le: 30 Avr 2008, 17:25
-
 par Matt_01 » 31 Oct 2008, 21:53
par Matt_01 » 31 Oct 2008, 21:53
Oula, pas évidente cette équation !
Faut-il utiliser le fait que :
^2+3(\frac{x-y}{2})^2)
Parce qu'à base de modulo je trouve pas grand chose, si ce n'est que
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
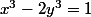
 = (3,3))
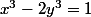

(x^2+x+1) = 2y^3)

=y^3)
=PGCD({x-1}{2}, 2x+1) = PGCD({x-1}{2}, 3})
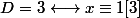 sinon
sinon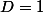
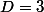
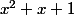 n'est jamais divisible par 9 (évident)
n'est jamais divisible par 9 (évident)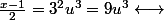
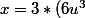 + 1 = 3k+1) (ici
(ici 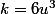 )
)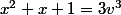
 + (3k+1) + 1 = 3v^3<br />\longleftrightarrow)
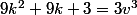

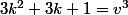

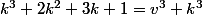

^3 = k^3 + v^3)
 ce qui donne la solution
ce qui donne la solution  = (1,0))
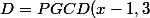 = 1)







 = y^3)
 = PGCD(u , 3))
 = 1) donc
donc  = 1) donc
donc  = 1)

 = 0)
)
 doit être un carré parfait. Ainsi :
doit être un carré parfait. Ainsi :


 est impair, donc
est impair, donc


) )
) ^3 < \beta^2 + \beta + 1 < ([\beta^{\frac{2}{3}}] + 2)^3)
 est compris entre deux cubes d'entiers successifs donc il n'est jamais un cube.
est compris entre deux cubes d'entiers successifs donc il n'est jamais un cube.