Ma solution :
Trouver toutes les solutions entières de
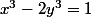
Supposons
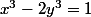

(x^2+x+1) = 2y^3)

=y^3)
or
=PGCD({x-1}{2}, 2x+1) = PGCD({x-1}{2}, 3})
donc
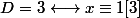
sinon
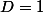
1) Cas
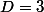
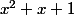
n'est jamais divisible par 9 (évident)
donc
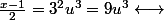
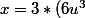 + 1 = 3k+1)
(ici
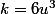
)
et
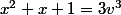
donc
 + (3k+1) + 1 = 3v^3<br />\longleftrightarrow)
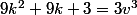

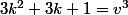

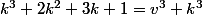

^3 = k^3 + v^3)
ce qui est impossible d'après le grand théoreme de fermat
2)Cas
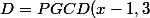 = 1)
x est impair donc
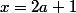
On a alors :
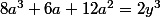
donc
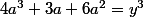
 = y^3)
or
 = 1)
car 3 ne divise par a (car 3 ne divise pas x-1 par hypothèse)
donc
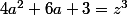
(z entier)
l'équation se réécrit :
^2 = z^3)
(notons que a est aussi un cube,
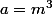
)
Etudions en général l'équation :
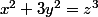
On se place dans

L'équation se réécrit :
(x-\sqrt{-3}z) = z^3)
or dans cet anneau, les deux facteurs sont premiers entres euxil exste donc u,v tels que
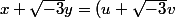^3)
en identifiant les parties réelles et imaginaires obtient
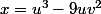
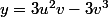
réciproquement :
^2 + 3(3u^2v - 3v^3)^2 = (u^2+3v^2)^3)
En revenant à notre équation :
^2 = z^3)
On obtient :
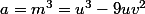
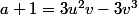
[/quote]
On a donc
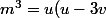(u+3v))
or
 = 1)
car
)
divise a et divise a+1.
et
 = 1)
(sinon, 3 divise m donc 3 divise a ce qui est exclu dans ce cas 2)
de plus u et v ont une parité différente sinon,
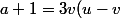(u+v))
et a auraient la même parité.
donc
 = pgcd(u,u+3v) = pgcd(u-3v,u+3v) = 1)
donc
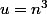
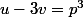

donc
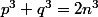
On a :
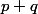
et
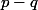
sont pairs car u et v sont de parité différente
donc
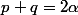
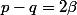
donc
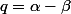
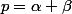
 = pgcd(p,q) = pgcd(u,v) = 1)
(facile à voir puisque
=pgcd(q,3) = 1)
)
en développant :
 = z^3)
donc
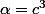
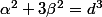
Mais
 < a^2 = (pqn)^6)
donc à l'équation
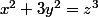
, en faisant le même raisonnement que précédemment, on construit une suite de solutions dont le carré est strictement décroissant, ce qui est impossible (descente infinie)
sauf si
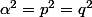
on obtient (car p et q premiers entres eux) alors n=0 donc u=0 donc a=0 donc (1,0) solution.