Equation de Cauchy sur un cercle

[Zweig]

Salut,

On dit que deux réels et sont égaux modulo 1, et on le note , lorsque .

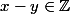
On considère la fonction continue telle que



Montrer qu'il existe tel que , pour tout .


Indication : On pourra utiliser le fait que les nombres dyadiques (nombres de la forme d = n*2^-m, n entier et m entier naturel) sont denses dans R.

[windows7]

salut,

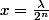
j'ai comme l'impression que c'est vrai pour tout avec
si c'est bien le cas suffit de constater que cet ensemble de nombre est dense dans [0,1[ et par continuité de f ...

c'est ca ou jsors une connerie ?

[Ben314]

Déjà, si tu veut avoir des chances de résoudre l'exo, il faudrait mieux rendre l'énoncé un peu moins "boiteux" :

On considère UNE fonction continue...

(il n'y a aucune raison qu'une telle fonction soit unique.

Est incohérent car f est définie sur [0,1[ et, lorsque x et y sont dans [0,1[, x+y n'est pas forcément dans [0,1].
A remplacer par :


Sans lequel on ne peut rien dire concernat par exemple f(1/2)+f(1/2) vu que 1/2+1/2 n'est pas dans [0,1[.

[Doraki]

[quote="windows7"]salut,

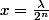
j'ai comme l'impression que c'est vrai pour tout avec [tex] \lambda 0, pour toute solution f continue ou pas, il existe un entier k tel que pour tout n > log2(;)), f(;)/2^n) = k;)/2^n"

Parceque pour tout > 0, il existe une solution f non continue telle que pour tout entier k il existe un n> log2(;)) tel que f(;)/2^n) k;)/2^n.

[Doraki]

J'ai une fonction solution qui n'est pas de la forme f(x) = nx [1] avec n dans N.

Ah et il ne peut même plus modifier son énoncé ! Que le forum est cruel !

[Ben314]

J'ai une fonction solution qui n'est pas de la forme f(x) = nx [1] avec n dans N.
Ah et il ne peut même plus modifier son énoncé ! Que le forum est cruel !

Avec f continue ?
Ca me surprend un peu...
Si on pose f(1/2^n)=an alors a(n+1)=an/2 ou bien a(n+1)=an/2+1/2 >= 1/2 mais la continuité de f en 0 et le fait que f(0)=0 impose que a(n+1)=an/2 pour tout n assez grand et on conclue rapidement.

[Doraki]

Quand on dit "fonction continue dans [0;1[", on considère qu'on est sur R/Z et pas sur la topologie usuelle de [0;1[ j'imagine.
(sinon y'a que 2 fonctions solutions et c'est pas très intéressant)

[Ben314]

Quand on dit "fonction continue dans [0;1[", on considère qu'on est sur R/Z et pas sur la topologie usuelle de [0;1[ j'imagine.

Effectivement, donc l'énoncé est encore plus bancale que ce que j'avais vu (je suis pas bien sûr que la notion d'esace topo quotient soit franchement vu en Lycée...)