équation avec intégrale

[wkj]

salut,

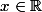déterminer toutes les fonctions f continues sur tels que pour tout on ai :

[Ben314]

Salut,
Sauf erreur, le terme de gauche est en O(x^2) lorsque x tend vers 0 donc ne peut être égal à x...

[wkj]

bien joué,

celle la :
(je l'ai posé sur le forum supérieur, et on m'a fait un truc en lien avec la transformée de fourier, est ce exact ?)

[wkj]

petit up, je trouve ca dommage que personne ne s'intéresse à ce genre d'équation.

[MacManus]

Bonjour,

Après quelques recherches, je trouve un rapport avec l'équation de Volterra de 1ère espèce. C'est une équation intégrale à noyau (différente de l'intégration dans les équations de Fredholm, en ce sens qu'elle est indéfinie) du type:



où K (Kernel) est le noyau, avec pour tout t > x, K(x,t)=0.

Il y a ce lien également, qui propose une solution pour une équation qui ressemble beaucoup à la tienne. Pour l'instant j'ai pas cherché à comprendre

[Ben314]

Je ne pense pas qu'il y ait un lien avec l'équation donné dans ton lien qui est plus ou moins un produit de convolution : lorsque t varie de 0 à x, x-t varie lui aussi de 0 à x (dans l'autre sens) alors que dans l'équation de wkj c'est du x+t qui varie de x à 2x...

Sinon, perso, j'aurais tendance à poser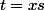 dans l'intégrale :

Et l'équation se réécrit
et là, il y a un "miracle" : la solution évidente (et la seule développable en série entière au voisinage de 0) de est 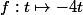et cette même fonction vérifie aussi donc c'est en fait une solution particulière de l'équation de départ.

Si pour tout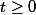 on pose alors , l'équation devient et, à mon avis, la seule solution "régulière" (???) de cette équation est la fonction nulle (à vérifier...)

[DamX]

Hello Ben,

wkj n'a même pas pris la peine de remettre ce qu'on lui avait vraiment dit dans l'autre fil http://www.maths-forum.com/showthread.php?t=156215, qui n'était pas une histoire de fourier qui ne menait à rien..

Tu as retrouvé d'une autre manière la même solution (f(x)=-4x) que ce que j'ai proposé et j'avais la même impression que la seule solution de l'équation "homogène" (celle qui donne = 0) soit la fonction nulle, mais ça ne m'avait pas l'air si évident à prouver (j'ai juste montré dans l'autre fil qu'elle s'annulait une infinité de fois entre 0 et 1/2 si elle est continue).

Damien

[MacManus]

Je ne pense pas qu'il y ait un lien avec l'équation donné dans ton lien qui est plus ou moins un produit de convolution : lorsque t varie de 0 à x, x-t varie lui aussi de 0 à x (dans l'autre sens) alors que dans l'équation de wkj c'est du x+t qui varie de x à 2x...

Oui tu as raison, je n'avais pas fait attention au produit de convolution dans mon lien.

Sinon, perso, j'aurais tendance à poser dans l'intégrale :

Et l'équation se réécrit
et là, il y a un "miracle" : la solution évidente (et la seule développable en série entière au voisinage de 0) de est et cette même fonction vérifie aussi donc c'est en fait une solution particulière de l'équation de départ.

Ok d'accord. pratique ce t=xs, ça facilite bien les calculs.