équation en arctan
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 28 Aoû 2006, 01:12
par nekros » 28 Aoû 2006, 01:12
Bonsoir,
Résoudre
+arctan(x)+arctan(x+1)=\frac{\pi}{2}})
Bonne réflexion.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 28 Aoû 2006, 01:28
par aviateurpilot » 28 Aoû 2006, 01:28

n'ai pas une solution
si
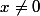
+arctan(x-1))=tan(\frac{\pi}{2}-arctan(x)))
+(x-1)}{1-(x+1)(x-1)}=\frac{1}{x})


S={

}
saut erreur
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 28 Aoû 2006, 01:33
par nekros » 28 Aoû 2006, 01:33
Hé bien, elle n'aura pas tenue longtemps celle là... :doh:
Reste à faire la réciproque.
A+
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 28 Aoû 2006, 01:42
par aviateurpilot » 28 Aoû 2006, 01:42
nekros a écrit:Reste à faire la réciproque.
pour
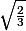
on a
+(\sqrt{\frac{2}{3}}-1)}{1-(\sqrt{\frac{2}{3}}-1)(\sqrt{\frac{2}{3}}+1)}=\frac{1}{\sqrt{\frac{2}{3}}})
donc
+arctan(\sqrt{\frac{2}{3}}-1))=\frac{1}{tan(arctan(\sqrt{\frac{2}{3}}))}=tan(\frac{\pi}{2}-arctan(\sqrt{\frac{2}{3}})))
par suite
+arctan(\sqrt{\frac{2}{3}}-1)=\frac{\pi}{2}-arctan(\sqrt{\frac{2}{3}}))
et la meme chose avec

non?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 04 Sep 2006, 21:53
par nada-top » 04 Sep 2006, 21:53
salut,
Nekros t'es sur que

est une solution, j'ai la flemme de reprendre les calculs d'aviateurpilote :mur:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 04 Sep 2006, 22:16
par nekros » 04 Sep 2006, 22:16
nada-top a écrit:salut,
Nekros t'es sur que

est une solution, j'ai la flemme de reprendre les calculs d'aviateurpilote :mur:
Non, il n'est pas solution.
Aviateurpilot aurait du continuer les calculs !
A+
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 04 Sep 2006, 22:26
par nada-top » 04 Sep 2006, 22:26
ok merci
car il m'est demandé de prouver que
 + Arctan(x+1) + Arctan(x) - \frac{\pi}{2})
est bijective , d'ou vient ma question.
@+
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 07 Sep 2006, 10:05
par le fouineur » 07 Sep 2006, 10:05
Bonjour à tous,
Je suis d' accord pour le résultat final,à savoir

,Mais comment faites-vous pour calculer le membre de droite de l'équation initiale,c'est à dire:
Tan[(Pi/2)-ArcTan(x)] car pour cette expression et en voulant apppliquer la formule d'addition des angles,il me semble qu'il y a une indétermination pour:

Comment faites-vous donc pour opérer sachant cette indéermination?
Merci de me répondre le fouineur
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 10:39
par nada-top » 07 Sep 2006, 10:39
Bonjour,
\right)=cotan(Arctan(x))=\frac{1}{tan(Arctan(x))}=\frac{1}{x})
;

@+
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 07 Sep 2006, 11:20
par le fouineur » 07 Sep 2006, 11:20
Bonjour nada-top et merci pour ta réponse rapide,
Je ne me souvenais plus de cette formule,qui établit un lien entre Tan et Cotan,il est vrai que durant toutes mes études,je n'ai jamais eu à l'utiliser....
Cordialement le fouineur
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 07 Sep 2006, 12:12
par nada-top » 07 Sep 2006, 12:12
de rien :happy3:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 12:19
par Flodelarab » 07 Sep 2006, 12:19
de rien :zen:
-
amine22
- Messages: 4
- Enregistré le: 20 Fév 2007, 20:10
-
 par amine22 » 13 Mar 2007, 20:13
par amine22 » 13 Mar 2007, 20:13
le fouineur a écrit:Bonjour nada-top et merci pour ta réponse rapide,
Je ne me souvenais plus de cette formule,qui établit un lien entre Tan et Cotan,il est vrai que durant toutes mes études,je n'ai jamais eu à l'utiliser....
Cordialement le fouineur
explicité le fonction
f(x)= somme de 1 à infini de (x^n/n^2) ?
et merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités