2 equa fonct
Olympiades mathématiques, énigmes et défis
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 02 Juil 2008, 15:58
par aviateurpilot » 02 Juil 2008, 15:58
salut tt le monde
dans ce qui suit
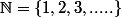
1) trouver toutes les fonctions
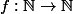
tel que
+f(m)|n+m)
2) trouver toutes les fonctions
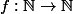
tel que
+f(m))
remarque: (1) est bcp plus facile que (2) lol.
bn courage
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 02 Juil 2008, 16:14
par lapras » 02 Juil 2008, 16:14
Salut
la (1) est évidente
supposons qu'il existe

tel que
>n_0)
on prend ici
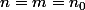
=>
 | n_0)
impossible
donc
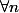
 \le n)
.
On suppose par hypothese de récurrence forte que
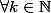
,
 = k)
Le postulat de bertrand dit qu'il existe

premier entre

et

donc entre

et
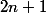
on prend
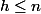
tel que
+h = p)
alors
 + f(h) = p)
(pas

car
 \geq 1)
)
or
 = h = p - (n+1))
donc
 = n+1)
par récurrence forte,
 = n)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 02 Juil 2008, 22:28
par aviateurpilot » 02 Juil 2008, 22:28
bravo lapras pour 1)
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 03 Juil 2008, 14:25
par lapras » 03 Juil 2008, 14:25
Mais tu n'as toujours pas précisé si on pouvait avoir m = n
si oui
pour 2),
)
=>
 = k*n)
réciproquement pour tout
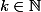
 = k*n)
est solution.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Juil 2008, 14:32
par aviateurpilot » 03 Juil 2008, 14:32
lapras a écrit:Mais tu n'as toujours pas précisé si on pouvait avoir m = n
si oui
pour 2),
)
=>
 = k*n)
réciproquement pour tout
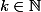
 = k*n)
est solution.
on px avoir

, il donne n|f(n) mais tous ce que tu px ecrire c'est
=g(n)n)
avec
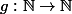
f(n)=k*n mais k n'est pas forcement une constante tu vois,
-
cacastor
- Messages: 2
- Enregistré le: 12 Juil 2008, 10:36
-
 par cacastor » 12 Juil 2008, 10:55
par cacastor » 12 Juil 2008, 10:55
Aviateurpilot es tu certain de la faisabilité du 2) , sinon je dirais que tout polynome à coefficients entiers qui n'admet que des puissances impaires convient, genre X^5+3X^9-X ou autre...Ca a l'air assez chaud sans hypothèses supplémentaires genre f est à croissance sous-pôlynomiale...
-
cacastor
- Messages: 2
- Enregistré le: 12 Juil 2008, 10:36
-
 par cacastor » 14 Juil 2008, 00:30
par cacastor » 14 Juil 2008, 00:30
Hello,
Je me permet de remonter ce topic car je trouve le 2) de aviateur pilote tès intéréssant et je déplore que peu de gens le cherchent...
Quelqun a t il une idée pour débuter?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités