Enigme : TAEG décalé !

[Anonyme]

Supposons un crédit de :

Capital K : 20.000 euros
Mensualités n : 60 mois
TAEG t : 4%

Quel en sera le montant de la mensualité m ?

Par application de la formule suivante :

M = K * t' / 1 - ( 1 + t' ) ^ [-n]
avec t' = tam * 12, le taux proportionnel
et tam = ( 1 + t ) ^ [1/12] - 1, le taux actuariel mensuel
(^ : exposant)
==> m = 367,68 euros

Voici l'énigme :

Lors d'un remboursement dit « différé »,
si nous décalons l'ensemble des mensualités d'un mois, que devient le TAEG ?

Sur base des mêmes éléments le TAEG sera de 3,87%,
mais quelle est la formule générale qui donne ce résultat ?

Quid si nous décalons de X mois ?

Go ! :o)

[Quidam]

Je ne suis pas familier avec ces formules bizarres, ni avec les vocables bidon qui les accompagnent. Pour moi, il n'y a qu'un seul taux mensuel : le t' de ta formule, que j'appellerai :

Et il n'y a qu'un seul taux annuel :
Il me semble que ce que j'appelle est précisément le TAEG (mais sans garantie). Les banquiers préfèrent annoncer le taux nominal () qui n'a aucune existence réelle dans les calculs, et n'a d'intérêt que pour minimiser le VRAI taux, qui est ce que j'appelle et ce que tu appelles TAEG. Dans les prêts à court terme, si le taux nominal est annoncé à 4%, le VRAI taux mensuel est 4/12 % et le VRAI taux annuel est soit 4.074 %. La différence ne semble pas gigantesque, mais du temps où le taux nominal - le taux minimisé annoncé par les banquiers) était 14% (il n'y a pas si longtemps), le VRAI taux était soit 14,93 % ! Et lorsque des usuriers vous proposent des taux de l'ordre de 1,5% par mois en ayant le culot d'annoncer 1.5*12 soit 18% pour des prêts à court terme, ils sont bien loin de la vérité car cela est en réalité du 19,56 % !

J'ai entendu dire que le sigle TAEG avait été imposé par Bruxelles pour uniformiser une pratique plus honnête largement répandue en Europe : dire simplement la vérité ! Désormais, au moins pour les prêts à long terme, les prêteurs doivent annoncer le VRAI taux soit ce que tu appelles TAEG et ce que j'appelle

Il me semble que dans la série de formules que tu indiques, tu fais des confusions :
[INDENT]Capital K : 20.000 euros
Mensualités n : 60 mois
TAEG t : 4%
M = K * t' / 1 - ( 1 + t' ) ^ [-n]
avec t' = tam * 12, le taux proportionnel
et tam = ( 1 + t ) ^ [1/12] - 1, le taux actuariel mensuel
(^ : exposant)
==> m = 367,68 euros[/INDENT]

Si le TAEG est de 4% alors tam = ( 1 + TAEG/100 ) ^ [1/12] - 1 (ce que j'appelle ) et dans la formule M = K * t' / 1 - ( 1 + t' ) ^ [-n] que tu indiques, c'est plutôt tam qui doit figurer à la place de t' :
M = K * tam / 1 - ( 1 + tam) ^ [-n]

En outre, quelle que soit la signification précise que tu donnes à t, t' et tam, la formule t' = tam * 12 suggère que tam est un taux MENSUEL, t' un taux ANNUEL et dans la formule M = K * t' / 1 - ( 1 + t' ) ^ [-n], t' est un taux "sur la période", c'est-à-dire, puisqu'il s'agit de mensualités, que t' serait alors un taux MENSUEL... Donc il y a des incohérences...

Si l'on a K=20000, n=60, M=367,68, alors le taux est égal à t=0.00327324445.... Ceci correspond à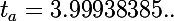
Il semble donc que le 4% que tu appelles TAEG correspond à ce que j'appelle

Inversement, avec un taux de 4% (soit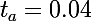 ), j'obtiens une mensualité de 367,6853...somme qu'il a fallu bien sûr arondir et cela donne le même résultat que toi : 367,68 euros.

Tout cela pour nous assurer que nous avons bien le même langage.

Pour répondre à ta question, je dirai qu'au lieu de la formule :


donnant la valeur de la mensualité M lorsqu'on emprunte une somme K à rembourser sur n mois avec un taux mensuel , il faut considérer que si l'on décale les remboursements de X mois, cela revient à laisser la somme K croître pendant X mois. K devient alors et alors, les n mensualités vont commencer. La formule à respecter est donc :


Comme, tu le sais, cette équation est du n-ième degré, n étant grand - en tous cas plus grand que 4 - il n'existe pas de méthode pour résoudre cette équation. La seule façon d'avoir une approximation est de faire un calcul itératif.

Pour savoir l'influence de X sur , toutes les autres variables étant constantes, il suffit de différencier cette formule !