Enigme suivante.
Olympiades mathématiques, énigmes et défis

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Avr 2018, 11:18
par Ben314 » 22 Avr 2018, 11:18
Salut,
(1) Montrer que, pour tout
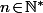
, le polynôme
\Big))
est à coefficients entiers.
(2) Exprimer
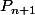
en fonction de

Modifié en dernier par
Ben314 le 22 Avr 2018, 16:03, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
mathelot
 par mathelot » 22 Avr 2018, 14:53
par mathelot » 22 Avr 2018, 14:53
-
nodgim
- Habitué(e)
- Messages: 2002
- Enregistré le: 27 Jan 2008, 10:21
-
 par nodgim » 23 Avr 2018, 06:48
par nodgim » 23 Avr 2018, 06:48
C'est quoi X dans l'histoire, SVP ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Avr 2018, 07:36
par Ben314 » 23 Avr 2018, 07:36
nodgim a écrit:C'est quoi X dans l'histoire, SVP ?
C'est la "variable" du polynôme.
Si tu voit Pn comme un polynôme formel, le X il représente rien du tout, mais comme on est dans R, ça change rien de voir Pn comme une fonction polynôme (style P(x)=3x²-5x+8) et dans ce cas, X c'est un réel.
Fondamentalement, la seule différence, c'est que, si tu voit ça comme une fonction, tu doit écrire
}\!=\!\!\prod_{k=0}^{n-1}\!\!\Big(x\!-\!2\cos\big(k\frac{2\pi}{n}\big)\Big)\ \text{et pas }\ P_n\!=\!\!\prod_{k=0}^{n-1}\!\!\Big(X\!-\!2\cos\big(k\frac{2\pi}{n}\big)\Big))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 23 Avr 2018, 10:05
par aviateur » 23 Avr 2018, 10:05
Bonjour
On a
/2+1=\cos(n \times arcos(x))=T_n(x))
c 'est à dire
=x p_{n+1}(x)-p_n(x)+2x -4)
ou encore
+2=x (p_{n+1}(x)+2)-(p_n(x)+2))
(pour tous machins et trucs dans ...)
d'où la réponse.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Avr 2018, 13:13
par Ben314 » 23 Avr 2018, 13:13
aviateur a écrit: /2+1=\cos(n \times arcos(x))}=\cdots)
Preuve ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 23 Avr 2018, 13:34
par aviateur » 23 Avr 2018, 13:34
J'aurai pensé que la preuve est évidente dans la mesure où l'on voit que p(2*x) et T_n(x)-1 on les mêmes racines et sont donc égaux à un facteur près et le facteur étant facile à trouver.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Avr 2018, 13:44
par Ben314 » 23 Avr 2018, 13:44
aviateur a écrit:J'aurai pensé que la preuve est évidente dans la mesure où l'on voit que p(2*x) et T_n(x)-1 on les mêmes racines et sont donc égaux à un facteur près et le facteur étant facile à trouver.
Sauf qu'il est bien clair que Pn admet des racines doubles donc il faut aussi montrer que ce sont des racines doubles de T_n(x)-1 si on veut pouvoir en en déduire qu'ils sont colinéaires.
Bref, c'est pas une évidence et ça demande une preuve (mais le principe est effectivement correct).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 23 Avr 2018, 14:36
par aviateur » 23 Avr 2018, 14:36
Ce n'est pas non plus compliqué à voir car cela vient de
-1)/dx =\dfrac{n \sin(n \times arccos( x)) }{\sqrt{1-x^2}})
et on fait attention aux détails.
-
aviateur
 par aviateur » 23 Avr 2018, 17:08
par aviateur » 23 Avr 2018, 17:08
Rebonjour
Une autre façon d'obtenir la récurrence (et donc le résultat) sans passer par les polynômes de Tchebychev
c'est de calculer le polynôme Q_n de degré 2n t. q
=x^nP_n(x+1/x)=\Prod_{k=0}^{n-1} (x^2-2 x cos(2k\pi/n)+1)=\Prod_{k=0}^{n-1} (x-exp(2 k\pi/n))((x-exp(-2 k\pi/n))))
D'où
=(x^n-1)^2)
On obtient alors
=x^n+1/x^n-2)
La récurrence vient donc de la formule
=(x+1/x)(x^{n+1}+1/x^{n+1})-(x^n+1/x^n))
-
mathelot
 par mathelot » 23 Avr 2018, 17:39
par mathelot » 23 Avr 2018, 17:39
aviateur a écrit: =x^nP_n(x+1/x)=\Prod_{k=0}^{n-1} (x^2-2 x cos(2k\pi/n)+1)=\Prod_{k=0}^{n-1} (x-exp(2 k\pi/n))((x-exp(-2 k\pi/n))))
ça ne serait pas des exponentielles complexes plutôt ?
-
aviateur
 par aviateur » 23 Avr 2018, 23:01
par aviateur » 23 Avr 2018, 23:01
il manque les i bien sûr

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Avr 2018, 10:20
par Ben314 » 24 Avr 2018, 10:20
aviateur a écrit:Une autre façon d'obtenir la récurrence (et donc le résultat) sans passer par les polynômes de Tchebychev
c'est de calculer le polynôme Q_n de degré 2n t. q
=x^nP_n(x+1/x)=\Prod_{k=0}^{n-1} (x^2-2 x cos(2k\pi/n)+1)=\Prod_{k=0}^{n-1} (x-exp(2 k\pi/n))((x-exp(-2 k\pi/n))))
D'où
=(x^n-1)^2)
On obtient alors
=x^n+1/x^n-2)
Je pense effectivement que c'est pas mal plus simple comme ça et en plus, ça permet de répondre facilement à la deuxième question.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 24 Avr 2018, 11:18
par aviateur » 24 Avr 2018, 11:18
Justement pour la deuxième question, on est bien d'accord que l'on a une relation de récurrence
entre P_{n+2},P_{n+1} et P_n mais pas de relation entre P_{n+1} et P_n. Sinon je ne vois pas cette relation.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Avr 2018, 11:51
par Ben314 » 24 Avr 2018, 11:51
Oui, la relation "naturelle", c'est une relation de récurrence linéaire d'ordre 2 (ou plutôt affine en ce qui concerne P_n) .
Mais il y en au aussi une (non linéaire bien sûr) d'ordre 1, i.e P_{n+1}=f(P_n).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 24 Avr 2018, 17:17
par aviateur » 24 Avr 2018, 17:17
Rebonjour
Comme relation je ne vois que ça:
=p_{n}\left(\cos\left(\frac{(1+n) \text{arccos}\left(\frac{u}{2}\right)}{n}\right)\right), u\in[-2,2])

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 24 Avr 2018, 19:01
par Ben314 » 24 Avr 2018, 19:01
Non, ça c'est pas une "formule de récurrence", c'est à dire c'est pas de la forme
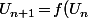)
vu que ta fonction

"contient" aussi du

.
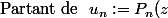\!+\!2<br />=P_n\big(x\!+\!x^{-1}\big)\!+\!2<br />=x^n\!+\!x^{-n},\ \text{ tu obtient :})
^2\!-\!u_n\,x^n\!+\!1\!=\!0\ <br />\text{ donc }\ <br />x^n\!=\!\dfrac{u_n\!\pm\!\sqrt{u_n^2\!-\!4}}{2}<br />\text{ et }<br />\ x^{-n}\!=\!\dfrac{u_n\!\mp\!\sqrt{u_n^2\!-\!4}}{2})
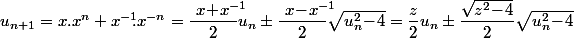
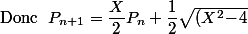P_n(P_n\!+\!4)}+(X\!-\!2)\;=\!\Phi(P_n)\ \text{ qui ne d\'epend que de }P_n)
Au vue des termes dominants, on peut préciser que le
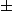
et un
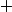
modulo de définir la racine carrée d'un polynôme unitaire (formel, qui est effectivement le carré d'un autre polynôme) comme étant le polynôme unitaire ayant comme carré celui de départ.
(par contre, en temps que fonction polynomiale de la variable réelle, je pense que ça sera pas systématiquement un 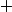 mais que ça dépendra du réel)
mais que ça dépendra du réel)Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 24 Avr 2018, 23:59
par aviateur » 24 Avr 2018, 23:59
Rebonjour
Je pense que si on fait le choix
P_n(P_n+4)})
avec
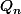
unitaire (i.e coeff dominant = 1)
au regard des coefficients dominant de part et d'autre de l'égalité il me semble bien que l' on doit mettre un plus quand x est grand.
Mais alors aussi pour tout
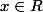
.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Avr 2018, 11:53
par Ben314 » 25 Avr 2018, 11:53
aviateur a écrit:Rebonjour
Je pense que si on fait le choix
P_n(P_n+4)})
avec
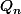
unitaire (i.e coeff dominant = 1)
au regard des coefficients dominant de part et d'autre de l'égalité il me semble bien que l' on doit mettre un plus quand x est grand.
Mais alors aussi pour tout 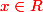
.
Pour x "grand" (et positif), O.K,. mais pas pour tout

:
Pour

réel
\!=\!x\!-\!2)
et la formule donne
<br />=\dfrac{1}{2}(x^2\!-\!4)\pm\dfrac{1}{2}\sqrt{(x^2\!-\!4)^2}=\dfrac{1}{2}(x^2\!-\!4)\pm\dfrac{1}{2}|x^2\!-\!4|\)
.
Or
\!=\!x^2\!-\!4)
, donc le
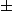
dépend de

: il faut prendre

si
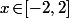
et
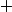
sinon.
(est-ce la même chose pour tout n ?)Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 25 Avr 2018, 14:02
par aviateur » 25 Avr 2018, 14:02
Je crois que l'on ne se comprend pas: le polynôme
 P_n( P_n+4))
est unitaire, c'est à dire que le facteur du coefficient dominant est égal à 1, le coefficient dominant est donc
)
il y a deux polynômes
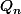
et
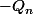
tels que
 P_n( P_n+4)=Q_n^2=(-Q_n)^2.)
l'un a pour coefficient dominant
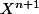
(il est unitaire c'est
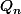
et l'autre a pour coefficient
dominant
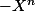
En posant
 P_n( P_n+4)})
alors nécessairement la formule de récurrence que tu as donné s'écrit avec un + et l'égalité de récurrence à est valable pour tout
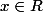
.
Pour n=2, pour moi
^2})
c'est donc
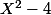
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
avec
unitaire (i.e coeff dominant = 1)
.