Énigme - Probabilités
Olympiades mathématiques, énigmes et défis
-
odin1700
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Jan 2019, 20:28
-
 par odin1700 » 06 Jan 2019, 12:24
par odin1700 » 06 Jan 2019, 12:24
Bonjour, je vous joint ci-contre cette énigme

Soit
)
la probabilité que les deux chats choisis aient la queue blanche

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Jan 2019, 13:40
par chan79 » 06 Jan 2019, 13:40
salut
soit

le nombre total de chats et

le nombre de chats à queue blanche
proba pour que les 2 tirés aient la queue blanche=
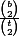
Cette proba est égale à 1/2 et ça donne
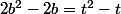
soit
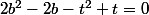
le discriminant de cette équation en b doit être un carré
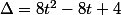
Comme elle a moins de 20 chats, seule possibilité:
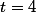
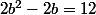
=6)
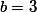
Elle a 4 chats dont 3 à queue blanche
-
odin1700
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Jan 2019, 20:28
-
 par odin1700 » 06 Jan 2019, 14:16
par odin1700 » 06 Jan 2019, 14:16
Bonjour,
Tout d'abord bravo pour la résolution de l'énigme, je voulais savoir comment vous déduisez de l'équation :
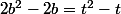
à partir des informations que vous avez
Merci

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Jan 2019, 15:12
par chan79 » 06 Jan 2019, 15:12
-
odin1700
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Jan 2019, 20:28
-
 par odin1700 » 06 Jan 2019, 15:38
par odin1700 » 06 Jan 2019, 15:38
J'avais compris cette égalité, mais est-ce que vous utilisez cette formule pour développer l'équation ?
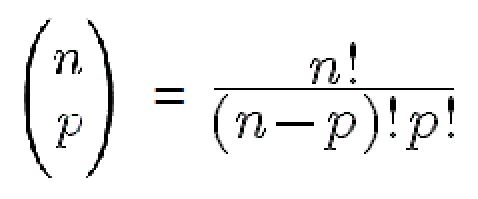

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Jan 2019, 15:40
par chan79 » 06 Jan 2019, 15:40
oui
-
odin1700
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Jan 2019, 20:28
-
 par odin1700 » 06 Jan 2019, 16:05
par odin1700 » 06 Jan 2019, 16:05
J'essaye de résoudre l'équation depuis tout à l'heure mais je n'arrive pas à arriver à votre équation finale
-
IntegerX
- Membre Naturel
- Messages: 31
- Enregistré le: 28 Déc 2018, 18:06
-
 par IntegerX » 06 Jan 2019, 16:32
par IntegerX » 06 Jan 2019, 16:32
Tu as C(2,b) / C(2,t) = 1 / 2. ( C(2,b) étant 2 parmi b)
Or C(2,b) = b! / (b-2)!*2! et comme b! = b*(b-1)*(b-2)! il y a une simplification qui s'opère et il ne reste que
C(2,b) = b*(b-1)/2.
De même pour C(2,t), d'où l'équation.
-
odin1700
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Jan 2019, 20:28
-
 par odin1700 » 06 Jan 2019, 17:21
par odin1700 » 06 Jan 2019, 17:21
Ah merci je ne connaissais pas cette équivalence merci
Par rapport au discriminant, je ne comprends pas d'où viennent les valeurs dans delta

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Jan 2019, 17:30
par chan79 » 06 Jan 2019, 17:30
delta=(-2)²-4*2(-t²+t)=8t²-8t+4
et il faut que ce soit un carré
on vérifie à la calculatrice ou avec un tableur (t<20)
-
odin1700
- Membre Naturel
- Messages: 39
- Enregistré le: 05 Jan 2019, 20:28
-
 par odin1700 » 06 Jan 2019, 18:36
par odin1700 » 06 Jan 2019, 18:36
Merci ça m'éclaire de plus en plus, mais pourquoi il faut que ce soit forcément un carré ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Jan 2019, 19:59
par chan79 » 06 Jan 2019, 19:59
Le nombre de chats b doit être un nombre entier.
Il est nécessaire que la racine de delta soit un entier.
S'il n'y avait pas la condition du nombre de chats inférieur à 20, il y aurait 21 chats dont 15 à queue blanche.
Mais 21 chats, ça fait beaucoup ...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Jan 2019, 21:17
par Ben314 » 06 Jan 2019, 21:17
Salut,
En fait, si
)
est une solution de
:2b(b\!-\!1)\!=\!t(t\!-\!1))
alors
\!=\!\big(3b\!+\!2t\!-2,4b\!+\!3t\!-\!3\big))
est aussi une solution de
)
et, partant de la solution "primitive"
\!=\!(1,1))
, on les obtient toutes par ce procédé :
\ \rightarrow\ (3,4)\ \rightarrow\ (15,21)\ \rightarrow\ (85,120)\ \rightarrow\ (493,697)\ \rightarrow\ (2871,4060)\cdots)
Et on peut même obtenir directement la

-ième solution
)
via les relation :
^{\!2n}\!\!+\!1\Big)\ \text{ avec }\ \varepsilon\!=\!\pm1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité