Énigme de 4 nombres

[voltech]

J'ai trouvé cette énigme sur le web et en plus mon prof me donne le même genre d'énigme, moi je sais pas comment trouver la réponse, est ce qu'il y a quelqu'un qui peut m'aider? Merci.



Existe-t-il 4 nombres qui, si on les combine par addition ou soustraction
(donc en prenant chaque nombre pour l'additionner ou pour le soustraire,
ou bien sans le prendre du tout)
permettent d'obtenir tous les nombres entiers
de 1 à 40 ? Si oui, quels sont ces 4 nombres ?

[Quidam]

Je propose 1, 3, 9 et 27

1 tout seul couvre trois nombres (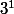) : -1, 0 et 1
3 tout seul couvre : -3, 0 et 3
Donc 1 et 3 ensemble couvrent :
(-1-3), (0-3) et (1-3) : -4, -3, -2
(-1+0), (0+0) et (1+0) : -1, 0, 1
(-1+3),(0+3) et (1+3) : 2, 3, 4

... soit les 9 nombres (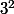) -4 à 4

9 tout seul couvre -9,0 et 9
Donc avec 1 et 3,
on peut couvrir -9 + (les 9 nombres de -4 à 4), soit -13 à -5
on peut couvrir 0 + (les 9 nombres de -4 à 4), soit -4 à 4
on peut couvrir +9 + (les 9 nombres de -4 à 4), soit 5 à 13

... soit les 27 nombres (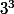) de -13 à 13

27 tout seul couvre -27,0 et 27
Donc avec 1,3 et 9,
on peut couvrir -27 + (les 27 nombres de -13 à 13), soit -40 à -14
on peut couvrir 0 + (les 27 nombres de -13 à 13), soit -13 à 13
on peut couvrir +27 + (les 27 nombres de -13 à 13), soit 14 à 40

... soit les 81 nombres (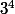) de -40 à 40