Enigme du Grand Père qui cherche...
Olympiades mathématiques, énigmes et défis
-
jufag
- Messages: 2
- Enregistré le: 21 Aoû 2010, 10:18
-
 par jufag » 21 Aoû 2010, 10:31
par jufag » 21 Aoû 2010, 10:31
Salut !
Je me présente rapidement j'ai pas vu de forum de présentation
Je suis Julien 28 ans, je suis de lyon ! Je suis de retour de vacances arfff lundi retour au taf !
Je suis passé par chez mon grand père on discutait et parlait du fait qu'on trouve presque tout sur internet ! Il m'a alors sortie un bout de papier sur le quel est noté une bien belle formule mathématique qu'il n'arrive pas à résoudre !
A 88 ans il me dit qu'il serait temps de demander de l'aide ! Il a demander à des prof de math qui lui ont tous dit impossible ! Hors mon grand père la sort d'un TP de math d'un élève qu'il avait eu en soutien scolaire !
Vous allez me dire ben l'élève à du avoir la correction ! C'est ce que j'ai pensé mais il ne l'a pas eu !
:help: Alors voila si vous avez un peu de temps voici le sujet :help: !

Merci mille fois d'avance de votre aide !
Je suis sur qu'il sera content si vous arrivez à lui expliquer !
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Aoû 2010, 10:56
par Finrod » 21 Aoû 2010, 10:56
Je commencerai par poser
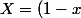^{1/3})
et
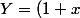^{1/3})
La relation donne
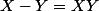
Et on aussi
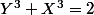
Bon après, je ne sais pas résoudre ce système mais ça à l'air faisable, au moins en valeur approchées.
-
Black Jack
 par Black Jack » 21 Aoû 2010, 13:13
par Black Jack » 21 Aoû 2010, 13:13
Petite erreur de signe pour Finrod.
Poser X = (1+x)^(1/3) et Y = (1-x)^(1/3)
X-Y = XY
X³ + Y³ = 2
X(1-Y) = Y
Y = 1 n'est pas solution -->
X = Y/(1-Y)
Y³/(1-Y)³ + Y³ = 2
Y³(1 + (1-Y)³) = 2.(1-Y)³
Y³ = (1-Y)³.(2-Y³)
Y³ = (1 - 3Y + 3Y² - Y³)(2-Y³)
Y³ = 2 - 6Y + 6Y² - 2Y³ - Y³ + 3Y^4 - 3Y^5 + Y^6
Y^6 - 3Y^5 + 3Y^4 - 4Y³ + 6Y² - 6Y + 2 = 0
Et c'est là qu'est l'os, on ne peut pas résoudre ce type d'équation (du moins analytiquement)
On le fait par exemple à la calculette et on trouve comme solutions réelles : Y = 1,148249... ou Y = 2,086438...
Et avec Y = (1-x)^(1/3), on a alors :
x = -8,0827... ou x = 0,8333...
Mais ce ne sont que des valeurs approchées des solutions.
:zen:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 21 Aoû 2010, 13:20
par Doraki » 21 Aoû 2010, 13:20
Un calcul compliqué donne x^6 + 6x^5 - 18x^4 - 4x^3 + 45x^2 + 6x - 28 = 0
Il y a deux racines réelles,
-8.08273917745471625604...
et 0.833316769885954358162...
ah ben grillé ^^'
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 21 Aoû 2010, 20:41
par Finrod » 21 Aoû 2010, 20:41
Enfin si la calculette fait la résolution, c'est qu'il y a un moyen.
Vous savez si c'est de l'optimisation ?
Comme la résolution par radicaux marchera pas.
-
Sve@r
 par Sve@r » 21 Aoû 2010, 20:42
par Sve@r » 21 Aoû 2010, 20:42
Doraki a écrit:Un calcul compliqué donne x^6 + 6x^5 - 18x^4 - 4x^3 + 45x^2 + 6x - 28 = 0
Il y a deux racines réelles,
-8.08273917745471625604...
et 0.833316769885954358162...
ah ben grillé ^^'
Je suis pas trop d'accord pour le -8.08
Pour moi, il n'y a qu'une seule racine en 0.833...

-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 21 Aoû 2010, 23:43
par uztop » 21 Aoû 2010, 23:43
Finrod a écrit:Enfin si la calculette fait la résolution, c'est qu'il y a un moyen.
je comprend pas cette phrase. La calculette ne trouve qu'une valeur approchée, ce qu'on peut faire aussi en traçant la courbe. D'ailleurs, je l'ai tracée sur ma Ti92 et on obtient bien deux racines (ton site soit bugger parce que la fonction varie trop rapidement autour de -8.08)
De façon générale, on ne peut pas résoudre par radicaux pour un degré supérieur à 5, donc c'est très probablement le cas ici.
-
Sve@r
 par Sve@r » 22 Aoû 2010, 00:35
par Sve@r » 22 Aoû 2010, 00:35
uztop a écrit:ton site soit bugger parce que la fonction varie trop rapidement autour de -8.08)
Exact. D'ailleurs ça se démontre très facilement (j'aurais du commencer par là)
f(-9)=65528
f(-8)=-3340
Etant donné que f est continue entre -9 et -8 (car somme de fonctions continues) elle est obligée de passer par 0. Comme quoi, faire trop confiance à la machine...
Et donc pour pouvoir visualiser cette courbe, m'a fallu modifier les échelles et
1) demander un affichage sur Y variant de -10000 à 10000
2) demander un pas de X de 0.0001
Et là, ça rend de suite qqchose de totalement différent...


-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Aoû 2010, 00:48
par Lostounet » 22 Aoû 2010, 00:48
Avec Géogebra, je vois uniquement le ~0.83.. (réglage 1:1).
En ajustant le réglage (1:500 voire 1:1000), je vois l'autre racine en -8,... Mais je pense que plus on 's'éloigne' du réglage initial, plus la courbe devient difficile à interpréter et floue..
J'ai fait un test avec une autre fonction: f(x) = x² - 9 par exemple, et la parabole qui 's'annule' normalement en 3 et -3 pour un réglage "normal" de 1:1 devient, pour un réglage de 1:500 ou 1:1000, complètement déformée et s'annule sur tout l'intervalle ~ [-10 ; 10] (ce qui est absurde..)
Déjà, on sait que la courbe représentative n'est pas tout à fait exacte et qu'elle fournit des valeurs approchées.. Et la modification des paramètres la rend encore plus floue..
Le -8.. est-il racine du truc finalement? Déjà que le 0,8.. est 'borderline' niveau exactitude.
Merci de m'expliquer pourquoi j'ai faux..!
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 22 Aoû 2010, 01:12
par Olympus » 22 Aoû 2010, 01:12
Faisable et élémentaire si c'était
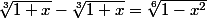
...
Là ça s'annonce un peu bourrin .
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 22 Aoû 2010, 08:11
par Finrod » 22 Aoû 2010, 08:11
uztop a écrit:je comprend pas cette phrase. La calculette ne trouve qu'une valeur approchée, ce qu'on peut faire aussi en traçant la courbe. D'ailleurs, je l'ai tracée sur ma Ti92 et on obtient bien deux racines (ton site soit bugger parce que la fonction varie trop rapidement autour de -8.08)
De façon générale, on ne peut pas résoudre par radicaux pour un degré supérieur à 5, donc c'est très probablement le cas ici.
Peut être. Je pensais à un algo de recherche de zéros
[url=http://fr.wikipedia.org/wiki/Algorithme_de_recherche_d'un_zéro_d'une_fonction]Lien[/url]
Qui est bien un moyen de trouver les valeurs approchées. Même si tracer la courbe et relever des données marche très bien. (mais l'algo doit être plus long).
-
Black Jack
 par Black Jack » 22 Aoû 2010, 15:46
par Black Jack » 22 Aoû 2010, 15:46
Si on veut faire une vérification graphique en évitant tout calcul, il suffit de tracer la courbe de f(x) = (1+x)^(1/3) - (1-x)^(1/3) - (1-x²)^(1/3)
... Et de voir pour quelle(s) valeurs(s) de x, elle coupe l'axe des abscisses.
On trouve bien les 2 solutions proposées.
:zen:

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 22 Aoû 2010, 16:01
par Olympus » 22 Aoû 2010, 16:01
Bizarre, Wolframalpha ne me donne qu'une seule solution à cette équation, le 0.83... ( et il précise clairement que c'est une racine du polynôme de Doraki ) .
Sinon, ce que je trouve encore plus bizarre, c'est ceci :
Hors mon grand père la sort d'un TP de math d'un élève qu'il avait eu en soutien scolaire !
Je ne sais pas comment on attend de cet élève de la résoudre, sachant qu'il n'y a rien d'astucieux ou de pédagogique dedans ...
Il y a donc sûrement une erreur dans l'équation je pense .

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 22 Aoû 2010, 16:48
par Lostounet » 22 Aoû 2010, 16:48
Olympus a écrit:Bizarre, Wolframalpha ne me donne qu'une seule solution à cette équation, le 0.83... ( et il précise clairement que c'est une racine du polynôme de Doraki ) .
C'est mon avis aussi, cf mon post précédent. :id:
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 22 Aoû 2010, 17:23
par Olympus » 22 Aoû 2010, 17:23
Lostounet a écrit:C'est mon avis aussi, cf mon post précédent. :id:
Je ne remettais pas en cause le fait qu'il y avait 2 solutions . Là je remets juste en cause l'efficacité de Wolframalpha, car notre fonction s'annule bien entre -8 et -9.
On pose
 = \sqrt[3]{1+x} - \sqrt[3]{1-x} - \sqrt[3]{1-x^2})
.
La fonction

est continue sur

( somme de fonctions continues sur le même intervalle ), et on a
 f\left( -8 \right) \simeq 0.15 \times \left( - 0.01 \right) < 0)
Donc d'après le théorème des valeurs intermédiaires,
=0)
admet bel et bien au moins une solution dans l'intervalle

.
Après, ce qui m'étonne c'est qu'un outil aussi avancé que Wolframalpha ( il utilise le même moteur que celui de Mathematica apparemment ) aie oublié la 2ème solution qui est de -8,..... .
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 22 Aoû 2010, 18:16
par Le_chat » 22 Aoû 2010, 18:16
La réponse vient de là :
[url]http://www.wolframalpha.com/input/?i=%281-x^2%29^%281%2F3%29[/url]
Wolfram ne considère comme à valeurs réelles la fonction
x:->(1-x^2)^(1/3) que dans [-1,1].
-
Black Jack
 par Black Jack » 22 Aoû 2010, 18:57
par Black Jack » 22 Aoû 2010, 18:57
Cà c'est malin, mais ne m'étonne pas...
Même si c'est faux.
:zen:
-
boumba daboum
- Membre Relatif
- Messages: 120
- Enregistré le: 07 Oct 2008, 15:31
-
 par boumba daboum » 23 Aoû 2010, 15:13
par boumba daboum » 23 Aoû 2010, 15:13
Avec Geogebra (excellent outil !), il suffit d'afficher la courbe (1+x)^1/3-(1-x)^1/3-(1-x^2)^1/3, de créer les points d'intersection avec l'axe des x, et d'augmenter le nombre de décimales affichées...
Il semble bien y avoir deux solutions, mais racine cubique de (1-8,0827), même si pour moi ça a un sens, on doit être obligé de l'écrire moins racine cubique de (8,0827-1)...
.

 par busard_des_roseaux » 24 Aoû 2010, 14:37
par busard_des_roseaux » 24 Aoû 2010, 14:37
Je pense avoir trouvé une solution si merveilleuse qu'elle ne tient pas dans la marge de la feuille . à ce soir , j'ai du taf. :hum:
signé Pierre de Fermat.
-
jufag
- Messages: 2
- Enregistré le: 21 Aoû 2010, 10:18
-
 par jufag » 26 Aoû 2010, 12:41
par jufag » 26 Aoû 2010, 12:41
Merci de toute vos réponses j'y connais mais rien de rien en math je vais déjà faire suivre vos recherches à mon grand père qui lui devrait comprendre bien mieux
Merci de vos réponses ! Pierre merci d'avance si vous avez trouvé une piste !!
J'envoi le lien des deux pages du forum à mon grand père par mail
J'ai tardé à vous remercier car les notifications par mail n'ont pas marché ou alors j'ai zapé un truc
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités




