L'Enigme Des Nombres Premiers est Enfin Resolu

[abdenimabdelaziz]

Bonjour,

J'ai l'honneur de partager avec vous mes recherches concernant les méthodes et les formules generatrices des nombres premiers de façon infinie, Leur Distribution ainsi que d'Autres Découvertes aussi Intéressantes.

cordialement

[pascal16]

Wello
c'est sympa de se poser toujours de questions toute sa vie.

Je n'ai regardé que le début pour l'instant.
Quand on recherche les nombres premiers, la méthode naïve à la calculatrice est de regarder si un nombre n est divisible par un nombre entre 2 et n
puis on améliore en s'arrêtant à sqrt(n)
puis on améliore en ne testant que 2 et les nombres impairs
puis on améliore en ne testant que 2, 3 et les nombres non multiple de 2, non multiples de 3. On obtient alors tes ensembles F et G de diviseurs possibles.
On ne va pas plus loin à la calculatrice, on n'optimise plus rien avec la complexification qui s'en suit.

[MMu]

Pour un béotien comme moi : qu'est ce qu'on a enfin résolu ?
Est ce qu'il s'agit d'une des nombreuses conjectures sur les nombres premiers

[nodgim]

Perso, j'ai eu la patience de regarder une centaine de pages du pdf. Beaucoup de tableaux et d'exemples, mais quid des maths là dedans ?
Il faudrait tout de même que l'auteur nous explique de quelle énigme sur les nombres premiers il parle, et laquelle il a résolu.

[Ben314]

Idem en ce qui me concerne : j'ai lu (en diagonale) pour y trouver comme seule "formule" mathématique que les nombres premier p>3 sont ceux de la forme 6k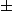1 auquel on "enlève" tout ceux qui peuvent s'écrire p=q*b avec q lui aussi de la forme 6k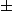1 et (en fait, c'est exactement ça les "suites arithmétiques" qu'il enlève)

Bref, des pages et des pages pour en arriver à la constatation qu'un nombre est premier ssi il n'a pas d'autre diviseurs que 1 et lui même (c'est à dire pour retomber sur la définition de nombre premier...)

AU MIEUX, on peut vaguement y voir la méthode du crible d’Ératosthène, et encore, on peut pas dire que ce soit franchement bien formulé : c'est plutôt le style "pourquoi expliquer avec des mots simples quand on peut le faire avec des mots compliquées". Par exemple de dire qu'on enlèves "les termes d'une suite arithmétique", plutôt que de simplement dire que, dès qu'on trouve un premier P on enlève les multiples de P autre que P (qui forment bien une suite arithmétique de premier terme 2P et de raison P), ben on peut pas dire que ça clarifie l'exposé...

[WillyCagnes]

bonjour,
Il m'a décomposé avec tous ces nombres composés....trop coloriés.... pour enfants

à l'âge de 12 ans j' étais heureux de trouver ma ptite formule sur les nombres Premiers
P²-1 est divisible par 24 (le jour de mon anniversaire)

(P²-1)/4! facilement demontrable de nos jours.