Encore une propriété du nombre d'or.

[Ben314]

Pour ceux qui ne passent pas sur le forum "supérieur", un problème donné à "jonses" :

1) Soit le nombre d'or.
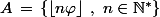
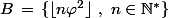
Montrer que et forment une partition de
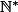
(où désigne la partie entière du réel )

Et il vient immédiatement à l'esprit la "réciproque" (si on peut dire) :

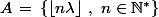
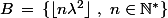
2) Soit un réel tel que et forment une partition de .
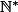
A-t-on forçément ?


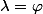
P.S. Je n'ai pas les réponses...

[nodjim]

2 très bonnes questions. Pour la partition, ça a l'air de bien marcher en tous cas. Et si c'est vrai, phi doit être le seul à faire ça: lambda plus fort laisserait des trous, plus faible donnerait des redondances...

[Imod]

Bonsoir Ben et Nodgim

Il s'agit d'un cas particulier du théorème de Beatty , non ?

Imod

[Ben314]

C'est fort possible.
Je ne connais pas le th. de beatty : je regarde...


(5' plus tard)
oui, c'est effectivement une application directe du théorème (pour les deux questions).

Je m'endormirais un peu moins idiot ce soir...

[nodjim]

Mince alors, c'est plutôt fort ce truc. Et effectivement ça donne directement la réponse aux 2 questions.
C'est court comme théorème et plutôt bluffant!
Bravo Imod pour ta réaction.