Encore un dégriseur . . .

[Ben314]

Salut,
En farfouillant dans les vielles énigmes, je suis tombé là dessus où, pour le moment, je suis assez sec pour la question 2.

On considère une grille () dont les cases contiennent des entiers naturels (un par case).
- On peut retrancher à n'importe entier de la grille modulo d'ajouter à tout les entiers voisins (4,3 ou 2 voisins selon que l'entier jouxte 0,1 ou 2 bords).
- On peut renouveler l'opération autant de fois que l'on veut tant que la grille contient au moins un entier bien sûr.

1) Montrer que, quelque soit la configuration initiale et quelque soit le choix des opérations, on fini par être bloqué.
2) Montrer que la situation finale (après blocage) et le nombre d'opération effectués (pour arriver au blocage) ne dépendent que de la configuration initiale et pas des choix fait pour les opérations.

EDIT : En fait, je pense avoir la solution aux deux questions mais en procédant de façon très différentes pour chacune d'elle.

[lyceen95]

La première étape, c'est de remarquer que l'ordre des opérations est sans effet. si je clique sur la case (a,b) puis sur la case (c,d), ou si je clique sur (c,d) puis sur (a,b), la situation obtenue est la même.
Ensuite, on remarque que si on clique sur différentes cases, si on regarde le rectangle qui contient ces différentes cases (le rectangle minimal qui contient ces cases), la somme des valeurs dans ces cases diminue forcément, parce que les clics sur des cases à la frontière de ce rectangle font diminuer la somme de toutes les valeurs.
Et donc sur une surface donnée, le nombre de clics est limité.

Il y a quelques trous dans la rédaction ; une bonne rédaction propre, complète est assez pénible à faire.

[Ben314]

Concernant la commutativité, ça serait correct si on avait le droit de mettre des négatif dans les cases, mais là, vu l'énoncé, il est possible que l'on ait le droit de faire (a,b) puis (c,d) mais qu'on ait pas le droit de faire le contraire ce qui fait qu'on ne peut pas se servir de cette "commutativité" comme bon nous semble.

Et concernant les rectangles, je ne suis pas sûr de comprendre pourquoi cette diminution de la somme sur certains rectangles (dépendant de où on a cliqué) implique la finitude du processus : peut-être en regardant les sommes sur TOUT les rectangles on pourrait aboutir à quelque chose, mais ça reste à démontrer.

Sinon, la preuve que j'ai pour la finitude n'est pas particulièrement "pénible" (4 ou 5 lignes quasi sans calculs). Pour la deuxième question, la méthode que j'ai est un peu plus chiantes à rédiger (mais toujours quasi sans calculs) et, à mon avis, il y en a une plus simple.

[Ben314]

En fait, ton histoire de rectangle, ça peut peut être marcher : si on regarde les cases qui jouxtent le bord du rectangle de départ R, quand on clique dessus, on perd 1 ou 2 sur la somme des valeurs de R donc, au maximum, on va cliquer sur ces cases là S fois où S=somme (au départ) sur tout le rectangle R.
Si on regarde maintenant le rectangle R' formé des cases qui ne jouxtent pas le bord de R, de même, quand on clique sur une case du bord de R', on perd 1 ou 2 sur la somme des valeurs de R' et, sachant que cette somme n'a pu être augmenté au max que S fois (de 1 à chaque fois) c'est qu'on a pu cliquer sur ces cases du bord de R', au maximum, que S+S' fois où S'=somme (au départ) sur tout le rectangle R'.
etc . . .

[lyceen95]

La commutativité : oui, une inversion n'est pas forcément autorisée, mais ce n'est pas cet aspect là qui m'importait. L'idée était de faire apparaître un invariant, ou une signature pour chaque position de départ : à partir d'une situation de départ, notons tous les mouvements possibles. Si une case a un nombre supérieur à 8 ( ou 12 ou ...), on note cette case, avec un coefficient 2. Cliquons sur toutes ces cases (en utilisant ces coefficients), peu importe l'ordre, on arrive toujours à la même situation.
Au passage, peut-être que de nouveaux mouvements sont devenus possibles. Dans ce cas, on recommence, et à nouveau, peu importe l'ordre.

Pour les rectangles, oui, l'idée est celle de ton dernier message. De proche en proche, on traite des rectangles de plus en plus petits. Je préfère le voir dans ce sens là : systématiquement, quand on peut cliquer sur une case à la frontière, on clique sur cette case.

Je suis bien conscient que mathématiquement, je ne démontre rien. Je dis juste : ça se voit que ces 2 résultats sont vrais.

Reste une propriété : le nombre de mouvements avant d'arriver au blocage est toujours le même. C'est la moins intuitive. On a l'impression qu'on peut répéter à l'infini en cliquant au centre, un peu comme des vases communicants. Mais après réflexion, cette propriété est vraie aussi.

Je reste sur ma conclusion : une bonne rédaction propre, complète est assez pénible à faire.

Par contre, essayer de trouver la position finale à partir d'une position initiale donnée, sans papier ni crayon, c'est un jeu qui va m'occuper un certain temps.

[Ben314]

Je peut t'affirmer que, si on s'y prend bien, ce n'est pas du tout "pénible" donc, que, comme dans tout bon casse tête qui se respecte, le but c'est de "bien s'y prendre" pour que "ce ne soit pas pénible" . . .

[Ben314]

Voilà une façon de procéder pas trop pénible pour la question 1 (il y en a surement d'autres éventuellement plus simples) :
On rajoute une ligne et une colonne sur chaque bord de façon à ne plus "perdre" des entiers lorsque l'on clique au bord (par contre, on ne clique pas sur ces cases). On numérote alors les lignes de à .
Quand on clique sur une case de la ligne ça retranche à la somme de la ligne et ça ajoute à et ce qui laisse invariant (ce qui était évident dés le départ...)
Par contre, le nombre augmente de .
Or, on a en permanence qui reste constant.

Remarque :
En fait, si on considère une forme quadratique quelconque ,
lorsque l'on clique sur une case, la quantité (où est le contenu de la case ) augmente de la constante
Mais, de façon générale, je ne sais pas déterminer l'ensemble des polynômes tels que
soit constant . . .

[Ben314]

Bon, vu que ça a pas l'air de déchaîner les foules et que j'aime pas les threads incomplets, ben je met une solution pour la deuxième question.

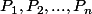
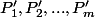
On part d'une situation de départ et on considère deux suites d'opérations et qui, partant de , donnent comme résultat final les situations et .
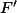
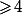
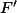
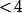
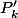
Si on regarde la case sur laquelle agit l'opération , dans la situation de départ , cette case doit contenir un entier . Or dans la situation finale cette case contient un entier donc l'une (au moins) des opérations est la même que .
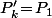
On enlève alors de la première liste ainsi qu'un des de la deuxième et on considère comme nouvelle situation de départ celle obtenue par l'application de à .
Ce faisant, on a toujours le même contexte, modulo que la deuxième suite d'opérations risque de "passer dans les négatifs".
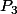
On recommence la même démarche avec (après avoir vérifié que le fait que la deuxième liste risque éventuellement de "passer dans les négatifs" ne modifie pas le raisonnement), puis , etc jusqu'à ce qu'on ait épuisé la première suite d'opération.
Le bilan, c'est que la deuxième suite devait, au départ, contenir tout les éléments de la première et au moins autant de fois chacun. Sauf que le processus étant symétrique (on aurait pu épuiser petit à petit la deuxième liste), ça signifie que les deux suites sont de même longueur et contiennent les mêmes opérations (et donc que les situations finales sont les mêmes).

Après, s'il y en a qui veulent chercher du pas mal compliqué (à priori), on peut chercher s'il y a un calcul (relativement) simple permettant de trouver quelle sera l'unique situation finale partant de celle de départ. J'ai un peu cherché dans la voie des systèmes linéaires sur Z/nZ (donc des trucs style "théorème des restes chinois"), mais sans arriver à grand chose.