Egnime et le côté incompréhensible des maths

[Anonyme]

Bon n'hésitez pas à poster des egnimes ou des mystères !
Voici mon egnime suivante :
0,999... C'est bien égal à 1, comme le sait-on, on ne peut rien placer entre les deux chiffre !
Pour ce qui ne savent pas Je vais expliquer :
0,99999...=1 on ne peut rien mettre entre les deux car les 9 sont à l'infini, on doit alors mettre 0 à l'infini mais comme les 0 sont infinis, où va-t-on mettre le 1 ? Comme on ne peut rien mettre entre les deux chiffres, Ils sont alors égaux.
J'en reviens sur mon 0,999... , comment les deux chiffre peuvent être égaux ?? Ils sont pas de la même values mathématiquement ! Entre 0,999... Et 1 il y a une différence infiniment PETITE . Mais on ne peut pas écrire ce chiffre !
MYSTÈRE.... Comment est-ce possible une telle égalité.

[leon1789]

C'est l'impact de l'infini.On peut se demander si l'infini est compréhensible, en effet.


Par ailleurs, essaie de faire la différence entre les chiffres et les nombres (exactement comme entre les lettres et les mots).

[Nightmare]

Beaucoup de choses ont déjà été dites dans la [url="http://www.maths-forum.com/0-9999-1-133362_5.php"]discussion[/url] à laquelle tu as toi-même répondu.

[Imod]

Bon n'hésitez pas à poster des egnimes ou des mystères !
Voici mon egnime suivante :
0,999... C'est bien égal à 1, comme le sait-on, on ne peut rien placer entre les deux chiffre !
Pour ce qui ne savent pas Je vais expliquer :
0,99999...=1 on ne peut rien mettre entre les deux car les 9 sont à l'infini, on doit alors mettre 0 à l'infini mais comme les 0 sont infinis, où va-t-on mettre le 1 ? Comme on ne peut rien mettre entre les deux chiffres, Ils sont alors égaux.
J'en reviens sur mon 0,999... , comment les deux chiffre peuvent être égaux ?? Ils sont pas de la même values mathématiquement ! Entre 0,999... Et 1 il y a une différence infiniment PETITE . Mais on ne peut pas écrire ce chiffre !
MYSTÈRE.... Comment est-ce possible une telle égalité.

Qu'un nombre ait plusieurs écritures je ne vois pas le problème . 1 a plusieurs écritures fractionnaires et ça ne gène personne . Il a deux écritures décimales dont une illimitée , il n'y a pas de quoi casser trois pattes à un canard .

Imod

[godzylla]

c'est une astuce, un trick play, 0.9999>0,999 toujours.
et 1+1=3?

[sylvain.s]

0.9999999999999999... = 1 ? comprend pas ^^

Même si les 9 sont ç l'infini, cela reste inférieur à 1 non ? :hum:

[Anonyme]

@sylvain.s

Il faut comprendre que la limite du nombre 0.9999999999999999... avec une infinité de décimales tend vers le nombre 1

Et on peut écrire que :



et que




Est ce que tu as compris quelque chose à ce message ?

[sylvain.s]

@sylvain.s

Il faut comprendre que la limite du nombre 0.9999999999999999... avec une infinité de décimales tend vers le nombre 1

Et on peut écrire que :



et que




Est ce que tu as compris quelque chose à ce message ?

Non je ne suis pas allé plus loin que le BAC s ^^;

Mais je ne comprend pas, si k tend vers + infini avec 9/ 10^k, je comprend que ca tend vers 1, mais j'arrive pas à m'imager que c'est égale, que ca tende oui mais ca atteind jamais 1.

Désolé si je fais mon boulet ^^, mais pour un simple bachelier c'est quand même abstrait ^^

[Anonyme]

@sylvain.s

Explications de ces 2 formules :

1)
c'est juste une notation pour "dire" que il y a une infinité de 9 dans l'expression 0.999...


2)

Soit la suite définie pas avec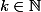
La suite est une suite géométrique

donc tu sais certainement calculer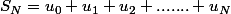

Une fois que tu as calculé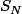
essaie de calculer la limite de "l'expression que tu as trouvé pour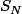 " quand tend vers +infini


ps)
En maths on écrit :

[Sylviel]

Une petite démonstration rapide
a = 0.99... (une infinité de 9)
alors
10a = 9.99...
10a-a = 9 (ben oui, la partie décimale de 10a et celle de a c'est bien la même, non ? parce qu'il y a une infinité de 9...)
9a=9
a=1

[sylvain.s]

Une petite démonstration rapide
a = 0.99... (une infinité de 9)
alors
10a = 9.99...
10a-a = 9 (ben oui, la partie décimale de 10a et celle de a c'est bien la même, non ? parce qu'il y a une infinité de 9...)
9a=9
a=1

La je comprend Merci syviel

@ptinoir : je suis désolé, mais avec la limites ca reste abstrait a mes yeux, ca tend vers mais c'est pas égale, mais j'ai du mal avec l'abstrait aussi :ptdr:

[Anonyme]

@sylvain.s

Les suites géométriques est une notion qui est au programme des classes de TS et TES

ainsi que le calcul de "la somme partielle" des N premiers termes d'une suite géométrique

c'est à dire de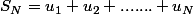


Dans mon message précédent :
Une fois que tu as fait tout le "travail" qui est très facile à faire pour un élève en classe de terminale TS ou TES ( voir en L ) qui connait son cours sur "les suites géométriques"


mon message nécessite juste de calculer la limite du terme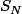 quand N tend vers +infini


ps)
La notion de "Limite en +infini" est aussi au programme des classes de TS et TES

[sylvain.s]

@sylvain.s

Les suites géométriques est une notion qui est au programme des classes de TS et TES

ainsi que le calcul de "la somme partielle" des N premiers termes d'une suite géométrique

c'est à dire de


Dans mon message précédent :
Une fois que tu as fait tout le "travail" qui est très facile à faire pour un élève en classe de terminale TS ou TES ( voir en L ) qui connait son cours sur "les suites géométriques"


mon message nécessite juste de calculer la limite du terme quand N tend vers +infini


ps)
La notion de "Limite en +infini" est aussi au programme des classes de TS et TES

J'ai comme l'impression que je te soule ^^, mais ce que j'essaye de t'expliquer c'est que dans ma tête je vois tres bien que la limite en + infini c'est 1, mais dans mon esprit ca tendra vers 1 sans jamais l'atteindre.

Ou alors j'ai mal compris la notion de limite, c'est possible aussi et c'est surement là que ca bloque

[Anonyme]

@sylvain.s

Non tu ne me soûles pas ( de toute façon , je bois toute la journée )

Tu as compris ce qu'est une limite et je conclurai par un simple : Bravo à toi !


Sinon pour les autres internautes qui n'ont pas encore compris

voici un Ptit conseil de Ptitnoir :

Faire l'exo sur la suite géométrique que j'ai proposé de faire et de travailler (voir dans cette discussion)
Cet exo permet de démontrer que 0,9999...... tend vers 1


ps1)

Je suis d'accord avec toi sylvain.s


"écrire le raccourci : 0,9999...... = 1 est VRAIMENT bof bof ,
car on n'explique RIEN avec cette égalité à part faire croire à certains élèves des choses qui ne sont pas vraies.... "

moi je dis bof bof bof ET bof...



ps2)

"Le bof bof bof ET bof" concerne l'égalité 0,9999... = 1


et



ne concerne pas sylvain.s



et ne lui est pas adressé !

[Kikoo <3 Bieber]

J'ai comme l'impression que je te soule ^^, mais ce que j'essaye de t'expliquer c'est que dans ma tête je vois tres bien que la limite en + infini c'est 1, mais dans mon esprit ca tendra vers 1 sans jamais l'atteindre.

Ou alors j'ai mal compris la notion de limite, c'est possible aussi et c'est surement là que ca bloque

Hello,

Juste avant d'aller me coucher (j'ai DS demain !), je voudrais discuter d'un truc intéressant que l'on a vu vite fait en cours avec mon prof : d'après le procédé diagonal de Cantor, il est impossible de "numéroter les réels". Donc nous pouvons en conclure qu'il est impossible d'intercaler un entier égal à 0 dans le développement décimal illimité de chaque réel (et donc que ce développement demeure "illimité"). Donc, chaque réel ne peut s'écrire que d'une unique manière dans un tel développement.
Je suis pas exactement sûr de la justesse de l'avant-dernière phrase, car on n'a fait que survoler cette anecdote en aparté, donc si quelqu'un voudrait bien compléter ou corriger, ce serait super
Dans le fond, cela permet de dire que 0,9999...=1.

En fait on était partis là-dessus quand j'ai demandé si des ensembles pouvaient être bien plus denses que d'autres dans , comme par exemple plus dense que . Puis après sur "il existe des infinis plus grands que d'autres", et tant que j'y pense, cela devrait faire plaisir à Dlzlogic de faire le point là-dessus

PS :

Donc nous pouvons en conclure qu'il est impossible d'intercaler un entier égal à 0 dans le développement décimal illimité de chaque réel (et donc que ce développement demeure "illimité")

N'importe nawak jusqu'à explication complémentaire !!
En tout cas je me souviens d'une fonction qui donnerait "x_n=0 si a_{nn}not=0 et x_n=1 si a_{nn}=0" ça vous dit qqchose ?

[Doraki]

Donc nous pouvons en conclure qu'il est impossible d'intercaler un entier égal à 0 dans le développement décimal illimité de chaque réel (et donc que ce développement demeure "illimité")

ça veut dire quoi ??? quel est le rapport avec la phrase précédente ??

[Kikoo <3 Bieber]

Ok, j'ai marqué un truc approximatif dans la marge, mais j'avais pas assez de place lol ^^
Bon ben je pense que je vais effacer cette ligne avant que tu fasses un infarctus :ptdr: