Disque entre 3 disques
Olympiades mathématiques, énigmes et défis
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 26 Sep 2010, 09:11
par nodjim » 26 Sep 2010, 09:11
Pas simple de trouver le rayon x d'un disque coincé entre 3 disques jointifs 2 à 2 de rayons a, b et c !
Inspiré de la question sur les cables électriques avec des diamètres de conducteur de tailles différentes...
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 26 Sep 2010, 19:09
par windows7 » 26 Sep 2010, 19:09
c'est le point de nagel ...
la construction est trivial, si on s'y prend bien le calcul du rayon l'est aussi.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 27 Sep 2010, 17:30
par nodjim » 27 Sep 2010, 17:30
Les figures que j'ai vues pour le point de Nagel ne correspondent pas tout à fait au problème posé, il me semble.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 28 Sep 2010, 17:18
par nodjim » 28 Sep 2010, 17:18
Pour l'instant, je n'ai pas pu trouver une équation directe f(a,b,c)=x.
Quelqu'un l'a t il ?
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
 par windows7 » 03 Oct 2010, 22:06
par windows7 » 03 Oct 2010, 22:06

la construction est simple, les calculs peut etre moins mais bon tu trouvera bien f(a,b,c)=r

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Oct 2010, 16:58
par Ben314 » 04 Oct 2010, 16:58

Si tu cherche juste la valeur de r, il suffit d'appliquer la loi des cosinus pour trouver les cosinus des trois angles "centraux" :
^2=(a+r)^2+(b+r)^2-2\cos(\gamma)(a+r)(b+r)\)
donc
=\frac{r^2+(a+b)r-ab}{(a+r)(b+r)}=1-\frac{2ab}{(a+r)(b+r)})
De même
=1-\frac{2ca}{(c+r)(a+r)}\)
et
=1-\frac{2bc}{(b+r)(c+r)}\)
Sauf que
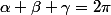
donc
+\cos^2(\beta)+\cos^2(\gamma)=1+2\cos(\alpha)\cos(\beta)\cos(\gamma)\)
ce qui, après quelques calculs, conduit à
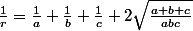
Modifié en dernier par
Ben314 le 14 Jan 2016, 22:04, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 04 Oct 2010, 17:17
par nodjim » 04 Oct 2010, 17:17
Super! je n'étais pas si loin, je n'avais pas pensé à la sommation des 3 cosinus.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités

