Diamètre d'un cable

par **landru** » 24 Sep 2010, 09:28

Bonjour.
Voilà mon problème: j'ai un cable contenant n brins. Chacun de ces bruns ont un diamètre différent. Les brins ne sont pas torsadés entre eux. Comment calculer le diamètre du cable?
Ça revient à calculer le diametre mini d'un cercle contenant des disques. Mais je bloque sur la méthode pour y arriver.

par **fatal_error** » 24 Sep 2010, 09:42

salut,

s'agit-il d'un problème concret, où d'un exo/énigme/défi?

par **Ericovitchi** » 24 Sep 2010, 09:51

la grande arme pour les histoires de cercles tangents c'est le théorème de Descartes qui lie les courbures des cercles.

Pour trouver de la littérature sur le sujet il faut chercher les mots "Kissing Circles" ou cercles de Soddy mais les gens se sont plutôt concentrés à rechercher des cercles à rayon entier ou à coordonnées des centres rationnels ou à des problèmes de coloriage

Mais là ton problème est un peu vague. Sans savoir le nombre de brins, ni grand chose sur les rayons des brins, je crains que l'on ne puisse pas dire grand chose.

par **landru** » 24 Sep 2010, 11:22

Mon problème est très concrêt. Je travaille dans le domaine industriel, plus particulièrement dans la conceptionde cables électriques. Ces câbles peuvent être à 3 brins de diamètres identiques comme à 100 brins de diamètres différents. Je veux pouvoir estimer le diamètre de mon câble avant de l'avoir fabriqué (au final, je veux automatiser mon calcul pour pouvoir le lancer sur une bonne cinquantaine de fois par semaine).
Dans un premier temps je vais regarder "kissing circle". Merci.

par **Ericovitchi** » 24 Sep 2010, 12:24

En fait il faudrait trouver un genre de formule empirique en utilisant par exemple la moyenne des diamètres de tous les brins (et peut-être l'écart type) de façon à avoir avec une bonne précision une approximation du diamètre global.

On peut déjà essayer de partir de la formule de Descartes pour 4 cercles
2(k1²+k2²+k3²+k4²)=(k1+k2+k3+k4)² et essayer de généraliser

par exemple les cercles tangents à 3 cercles de courbure k1,k2,k3 c'est

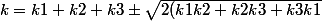En généralisant cette formule à n cercles on aura peut-être la bonne surprise de voir que ça n'est pas trop faux ?

par **Ericovitchi** » 24 Sep 2010, 12:53

Autre approche possible à caractère plus expérimental.
Si tu as des exemples de réalisation. Tu positionnes les points ("diamètre moyen des brins" x n (ou mieux la section en mm² car dans les catalogues de câbles électriques c'est plutôt la section de cuivre qui est marquée) ; diamètre global du câble) dans un repère et tu regardes s'il y a une bonne corrélation dans ce nuage de points. Si ça ressemble même vaguement à une droite, tu calcules la droite de régression et ça te donnera une formule.

par **landru** » 24 Sep 2010, 14:21

Avec toutes ces infos, mon axe de recherche est le suivant : je trie les brins du plus gros au plus fin. Ensuite je construit un premier triolet avec la formule de décarte (2 disques + 1 enveloppe) et j'essaie de remplir les sites si possible, sinon j'aggrandis l'enveloppe.

par **Ben314** » 24 Sep 2010, 15:54

Salut,
Si tu compte informatiser le chmilblick, une aproche "empirique" peut être suffisante : tu place le plus gros fil centré en (0,0) puis, en prenant les autres fils un aprés l'autre, tu fait regarder à l'ordinateur où est-ce qu'il doit positionner le fil de façon à ce que le diamètre global soit le plus petit possible (je pense que faire un tel algorithme n'est pas super super compliqué).
Ensuite, tu fait appliquer à l'ordinateur cet algo plusieurs (un grand nombre) de fois en changeant l'ordre dans lequel il prends les fils (j'aurais tendance à les prendre du plus grand au plus petit, mais je pense qu'il faut absolument faire plusieurs essais si on veut avoir des chances d'avoir une solution pas trop loin de l'optimum).
Ce type de solution conduit en général à des résultats "assez satisfaisants" bien que l'on puisse difficilement dire de façon théorique que écart il y a entre le placement trouvé par l'ordi et le placement "optimum"

par **benekire2** » 24 Sep 2010, 16:02

Je me demande, est-ce que théoriquement il y a des méthodes qui peuvent donner le diamètre minimum d'un tel cercle contenant plusieurs cercles ? C'est assez intéressant mais loin d'être évident à mon goût. Je ne connias pas non plus d'outils appropriés ...

par **Ben314** » 24 Sep 2010, 16:57

Je ne sais pas s'il existe des algorithmes utilisables pour résoudre ce problème, mais, cela ressemble suffisamment au problème du "voyageur de commerce" pour me convaincre de na pas chercher dans cette voie dés que le nombre de fils dépasse la douzaine (i.e. de ne pas chercher LE optimum, mais seulement une solution pas trop pourrie...)

par **benekire2** » 24 Sep 2010, 17:39

Donc en fait tu es sûr qu'il n'y a pas de méthodes n'utilisant aucun algorithmes pour résoudre ce genre de problèmes... ça me choque pas tellement en fait, mais j'avais espéré qu'il en existait une :cry:

par **Imod** » 24 Sep 2010, 22:29

Je n'y connais vraiment rien mais je dans le style empirique , je verrais bien une expérimentation du style : encerclé une poignée de spaghetti avec un élastique . Mais bon ce ne ne sont plus des maths :hum:

Imod

par **Ben314** » 24 Sep 2010, 22:44

Pour Bene : je ne suis absolument pas "sûr" qu'il n'y ait pas de jolie méthode...
Pour Imod : O.K. c'est pas vraiment des math, mais il est souvent surprenant de constater qu'avec des spaghettis et un élastique (en secouant un peu ET en testant un certain nombre de positions initiales) on obtient souvent des solutions assez satisfaisantes...

par **landru** » 24 Sep 2010, 23:29

Je compte informatiser la méthode. Mais les mathssont un peu loin derrière moi, et je cale unpeu pour calculer les deux solution de coordonnées du centre d'un cercle tangent à deux autres. Il est vrai que je ne cherche pas l'arrangement optimum, car dans la vrai vie mes brins ne prendront pas des positions totalement optimum. D'ailleurs je compte appliquer une tolérence au diamètre de chaque brin pour palier à cet écart d'arrangement.

par **windows7** » 25 Sep 2010, 09:48

Ben314 a écrit:Je ne sais pas s'il existe des algorithmes utilisables pour résoudre ce problème, mais, cela ressemble suffisamment au problème du "voyageur de commerce" pour me convaincre de na pas chercher dans cette voie dés que le nombre de fils dépasse la douzaine (i.e. de ne pas chercher LE optimum, mais seulement une solution pas trop pourrie...)

y'a eu une medal field pour ca xD

par **nodjim** » 25 Sep 2010, 10:01

landru a écrit:Mon problème est très concrêt. Je travaille dans le domaine industriel, plus particulièrement dans la conceptionde cables électriques. Ces câbles peuvent être à 3 brins de diamètres identiques comme à 100 brins de diamètres différents. Je veux pouvoir estimer le diamètre de mon câble avant de l'avoir fabriqué (au final, je veux automatiser mon calcul pour pouvoir le lancer sur une bonne cinquantaine de fois par semaine).
Dans un premier temps je vais regarder "kissing circle". Merci.

Je suis très curieux de connaitre dans quel domaine on a besoin de fabriquer des cables électriques dont les conducteurs sont de diamètre différent.

par **nodjim** » 25 Sep 2010, 10:06

Sinon, dans le même ordre d'idée, quel est le carré mini dans lequel on peut mettre 2, 3, 5,... disques de diamètre 1 ?
La réponse est très expérimentale, plus physique que mathématique....

par **landru** » 27 Sep 2010, 10:13

nodjim a écrit:Je suis très curieux de connaitre dans quel domaine on a besoin de fabriquer des cables électriques dont les conducteurs sont de diamètre différent.

Aéronautique. Mais les mêmes problèmes se posent dans l'automobile et peut-être même dans le naval. Dès qu'il y a des câbles customisés dans un environnement où l'espace coûte cher, il faut pouvoir estimer les diamètres.

par **windows7** » 30 Sep 2010, 08:46

correction : prix nobel, et non pas medal field.

Diamètre d'un cable

diamètre d'un cable

Qui est en ligne