Ben314 a écrit:Pour la somme, on a directement :
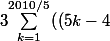+(5k-3)+(5k-2)-(5k-1)-5k\right)<br />=\sum_{k=1}^{402}(5k-8)=5\frac{402\times403}{2}-8\times 402=401799)
Exactement, il suffit de regarder chaque terme modulo 5 ^^
@darkpseudo : Pour les facto, à force de travailler plusieurs inégalités, on garde en tête pas mal d'identités "remarquables" . Pour identifier ce qu'il faut factoriser par contre, j'utilise Muirhead et Schur comme "testeurs" pour séparer les termes qui paraissent positifs, puis je factorise .
Pour le 3ème, s'il nous était demandé de trouver seulement les fonctions continues dans R vérifiant la relation là, alors il suffirait de prouver, dans le cas où
 = 1)
, que
=p)
pour tout
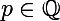
pour ensuite déduire que
=\lim f\left( x_n \right) = \lim x_n = x)
où
)
est une suite de rationnels et dont la limite est
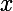
( l'existence de cette suite est vérifiée par la densité de Q dans R ) .
Enfin, f est forcément continue vu que les solutions ( la fonction nulle et l'identité ) le sont, mais je ne vois pas comment le prouver sans chercher à trouver ces solutions ...
Sinon, la solution par tâtonnements ( un peu proche de celle de FF, la sienne étant plus jolie :we: ) :
Il est relativement facile de vérifier que
=0)
, et ensuite, dans le cas où
 \neq 0)
, que
 = 1)
et que
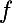
est impaire .
Toujours dans le cas où
 \neq 0)
:
On montre aussi que
 = f\left(x\right) + 1)
( en remplaçant
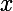
par 1 et
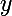
par
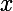
) .
On a
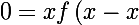 = xf\left(x\right) + f\left(x^2\right) f\left(-1\right) = xf\left(x\right) - f\left(x^2\right))
.
Donc
=f\left(x^2\right)=f\left(x\left(x-1+1\right)\right) = f\left(x\right) \left( 1 + f\left(x-1\right) \right) = f\left(x\right) \left( 1+ f\left(x\right) - 1 \right) = \left( f\left(x\right) \right)^2)
.
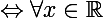
:
 = 0)
OU
 = x)
.
EDIT ( correction ) : ensuite, il faut montrer que
 \neq 0)
, ce qui est vrai car
 \left( 1 + f\left( \frac{1-x}{x} \right) \right) = f\left( x + 1 - x \right) = f\left(1\right) = 1 \neq 0)
.
Maintenant, dans le cas où
=0)
:
On aura immédiatement
=0)
, dont la solution est tout simplement la fonction nulle, qui vérifie bien l'énoncé .
