Deuxième test marocain 2011

par **Olympus** » 04 Déc 2010, 18:45

ffpower a écrit:Olympus : je n'ai pas compris ton passage f(x(x-1+1))=f(x)(1+f(x-1)) ( edit : c'est bon j'ai compris en fait )
Et la fin n'est pas tout a fait finie : tu obtiens "pour tout x, f(x)=0 ou f(x)=x", mais il faut arriver à : "pour tout x f(x)=0" ou "pour tout x f(x)=x"

Ah ouais la boulette, pas fait attention au quantificateur :briques:

Dans ce cas, il suffirait de montrer que pour tout

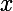
non nul,

. On suppose qu'il existe un réel

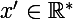
tel que

. Puis on aura

, contradiction vu que

.

( bien sûr, nous parlons du premier cas ici )

par **tarask** » 04 Déc 2010, 19:41

benekire2 a écrit:OK, mais bon, là chebychev sert a rien pour la gauche, on aurait pu mettre du cauchy schwarz ou même refaire ces carrés soit même . C'est pour la droite que ça coince.

Bonsoir !
Oui , c'est bien ça ce que j'ai fait !
avec C.S: (ab+ac+bc)(1/ab +1/ac+1/bc)>= 9 (ab+ac+bc)[(a+b+c)/abc]>=9 et on conclut en sachant que a+b+c=1.
pour l'autre côté , j'ai utilisé schur pour t=1 qui donne immédiatement ab+ac+bc<(1+9abc)/4 (puisque a+b+c=1 ) et on conclut facilement.
Le premier exercice , je donne la même solution que j'ai avancée dans un autre forum :

par **Rifi63** » 05 Déc 2010, 18:14

Olympus peux-tu me dire c'est koi Schur stp ?

par **Olympus** » 05 Déc 2010, 18:21

Salut !

@Rif63 : Tu peux regarder ici http://www.artofproblemsolving.com/Wiki/index.php/Schur's_Inequality ^^

par **Rifi63** » 06 Déc 2010, 23:00

Olympus a écrit:Salut !

@Rif63 : Tu peux regarder ici http://www.artofproblemsolving.com/Wiki/index.php/Schur's_Inequality ^^

Merciiiiiii

Deuxième test marocain 2011

Qui est en ligne