Deux sommes de Riemman
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 15 Aoû 2006, 22:21
par nekros » 15 Aoû 2006, 22:21
Salut,
Déterminer :
**
}}{n^2}))
**
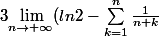^{\frac{1}{n+1}})
Bon courage !
A+
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Aoû 2006, 12:55
par Nightmare » 16 Aoû 2006, 12:55
Salut Nekros :happy3:
J'ai une vague idée de raisonnement pour la première, je n'ai pas le temps de m'étaler je dois aller bosser.
On note :
}}{n^{2}})
En appliquant le logarithme népérien :
=\Bigsum_{k=1}^{n} ln(1+\frac{\sqrt{k(n-k)}}{n^{2}}))
On sait que au voisinage de 0 :
\sim x)
On pourrait alors en déduire que :
}}{n^{2}})\sim \Bigsum_{k=1}^{n} \frac{\sqrt{k(n-k)}}{n^{2}}\longrightarrow_{n\infty} \Bigint_{0}^{1} \sqrt{x(1-x)}dx=\frac{\pi}{8})
Je verrai ça ce soir
:happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Aoû 2006, 13:13
par Nightmare » 16 Aoû 2006, 13:13
Non j'ai dit n'importe quoi, mais l'idée est là :lol2:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 17 Aoû 2006, 14:24
par nekros » 17 Aoû 2006, 14:24
C'est vrai que l'idée est là, puisque tu trouves la bonne limite :++:
Tu tentes la suivante ?
A+
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 20 Aoû 2006, 20:44
par kazeriahm » 20 Aoû 2006, 20:44
euh ca fait pas 0 pour la deuxieme ?
la limite de la somme des 1/(n+k) est ln 2 ... ?
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 20 Aoû 2006, 21:07
par Huit » 20 Aoû 2006, 21:07
Bonjour,
J'ouvre une petite parenthèse au sujet mais j'aimerais savoir ce qu'est une somme de Riemman ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2006, 21:24
par Nightmare » 20 Aoû 2006, 21:24
Bonsoir Huit :happy3:
On appelle somme de Riemann associée à une fonction f sur l'intervalle [a,b] une somme de la forme :
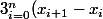f(\xi_{i}))
où les

appartiennent à la subdivision de pas n de l'intervalle [a,b] et

Les sommes de Riemann tendent vers l'intégrale de f sur l'intervalle [a,b]
:happy3:
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 20 Aoû 2006, 21:26
par ayanis » 20 Aoû 2006, 21:26
C'est un moyen de donner une définition rigoureuse de l'intégrale sur un intervalle. tu découpes ton intervalles en une subdivision de pas 1/n avec n grand, tu prends des x1, ... xn dans chacun de ses intervalles et tu prends la valeur f(xi). Tu défini alors l'integrale de f sur l'intervalle comme la somme de Riemann des f(xi) du coup, tu calcule l'aire sous la courbe d'une fonction en escalier et quand tu fais tendre n vers plus l'infini ca te donne la valeur de l'intégrale...
Je sais pas si j'ai été très claire. En gros c'est ce qu'on utilise en terminale sans en donner le nom pour définir une intégrale à partir d'une fonction en escalier proche de la fonction de départ...
Voili, voilou :we:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 20 Aoû 2006, 21:51
par nekros » 20 Aoû 2006, 21:51
kazeriahm a écrit:euh ca fait pas 0 pour la deuxieme ?
la limite de la somme des 1/(n+k) est ln 2 ... ?
Salut,
Non la limite n'est pas 0 :triste:
A+
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 20 Aoû 2006, 21:59
par Nightmare » 20 Aoû 2006, 21:59
Jolie forme indeterminée en tout cas ... Je m'y suis penché sans rien trouver pour le moment, en fait je ne sais pas comment la lever pour le moment, peut être avec un équivalent...
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 20 Aoû 2006, 22:09
par Huit » 20 Aoû 2006, 22:09
Merci à vous pour les précisions.
Ce fut clair, je pense avoir compris ! :)
Bon courage dans la résolution de cet exercice qui dépasse mon niveau !
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 20 Aoû 2006, 22:37
par nekros » 20 Aoû 2006, 22:37
Salut Nigthmare,
Je ne sais pas si ça se résout avec les équivalents, peut-être...
En tout cas, une autre méthode consiste à considérer l'application f qui à x dans

associe
=\frac{1}{1+x})
dans
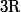
Ensuite, tu montres que f est 1-lipschitzienne (désolé pour l'orthographe :lol5:) et tu étudies :
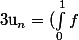-\frac{1}{n} \sum_{k=1}^{n} f(\frac{k}{n}))
, notamment en majorant sa valeur absolue.
A+
-
ayanis
- Membre Relatif
- Messages: 234
- Enregistré le: 19 Aoû 2006, 21:22
-
 par ayanis » 20 Aoû 2006, 23:00
par ayanis » 20 Aoû 2006, 23:00
nekros a écrit:Salut Nigthmare,
lipschitzienne (désolé pour l'orthographe :lol5:)
A+
Le pire c'est que tu l'as bien orthographié! :ptdr:
:++:
franchement chapeau! :we:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 20 Aoû 2006, 23:11
par nekros » 20 Aoû 2006, 23:11
ayanis a écrit:Le pire c'est que tu l'as bien orthographié! :ptdr:
:++:
franchement chapeau! :we:
:ptdr:
C'est bien la première fois ! J'hésite toujours entre trois orthographes...
Merci pour la précision.
A+
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 21 Aoû 2006, 00:58
par kazeriahm » 21 Aoû 2006, 00:58
beuh je comprends pas, nekros, ta suite (Un) va tendre vers 0, par définition de l'intégrale de Riemann... le problème étant l'exposant, je vois pas en quoi ca aide...
pouvez vous eclairer ma lanterne?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 21 Aoû 2006, 11:06
par Nightmare » 21 Aoû 2006, 11:06
Kazeriahm > C'est une forme indeterminée du type

-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 21 Aoû 2006, 12:13
par kazeriahm » 21 Aoû 2006, 12:13
oui nightmare, merci... :we:
je disais juste que je ne comprenais pas en quoi
nekros a écrit:Ensuite, tu montres que f est 1-lipschitzienne (désolé pour l'orthographe :lol5:) et tu étudies :
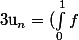-\frac{1}{n} \sum_{k=1}^{n} f(\frac{k}{n}))
, notamment en majorant sa valeur absolue.
apportait une aide au problème, on va montrer que Un converge vers 0 -> intégrale de Riemann, youpi
-
kazeriahm
- Membre Irrationnel
- Messages: 1608
- Enregistré le: 04 Juin 2006, 09:49
-
 par kazeriahm » 21 Aoû 2006, 18:43
par kazeriahm » 21 Aoû 2006, 18:43
la deuxieme converge vers 1, il faut encadrer la somme de riemann en question par deux autres sommes
je posterai la demo demain si a personne ne l'a fait d'ici la :we:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 23 Aoû 2006, 15:36
par nekros » 23 Aoû 2006, 15:36
kazeriahm a écrit:la deuxieme converge vers 1, il faut encadrer la somme de riemann en question par deux autres sommes
je posterai la demo demain si a personne ne l'a fait d'ici la :we:
J'attends ta démo kazeriahm. :zen:
A+
-
buzard
- Membre Relatif
- Messages: 274
- Enregistré le: 22 Mai 2006, 14:29
-
 par buzard » 23 Aoû 2006, 16:19
par buzard » 23 Aoû 2006, 16:19
avec un simple développement asymptotique on s'en tire aussi.
La série harmonique se développe en :
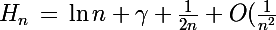)
on a donc que :
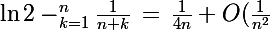)
On en déduit aisément la limite
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
, notamment en majorant sa valeur absolue.