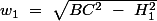SOLUTION 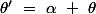
avec :
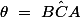
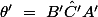

car sinon ou alors x=0 or ici x=2
ou alors ABC n'est pas un triangle
on obtiens :
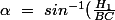)
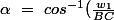)
avec le systeme de trois equations à trois inconnues réelles et strictements positives

et

et

à résoudre :
.(\ T_1-\sqr{(BC+x - w_1)^2\ +\ H_1^2}<br /><br />\ ).(T_1-BC-x)}{(BC+x)^2})
^2\ +\ H_1^2}}{2})
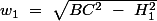
Pour la resolution du systeme heu...
une autre fois heu...milles excuses... :ptdr:
Bon sinon à part ça on peut faire
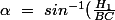\ =\ \frac{\pi}{2}\ - cos^{-1}(\frac{H_1}{BC}))
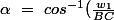)
Donc
\ =\ cos^{-1}(\frac{w_1}{BC})<br />\)
mais aussi selon
 \ +\ cos^2(\alpha) =\ 1\)
et
 \ =\ \frac{H_1}{BC}\)
et
 \ =\ \frac{w_1}{BC})
alors
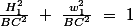
alors
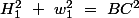
donc
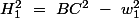
ça nous avance pas beaucoup!
Non! ... J'y réchappe pas avec mon systeme pourri de trois equations initial
méthode :
1)le coté AC (on aurait pu choisir aussi BC mais bon aucune importance il faut choisir)
2)la hauteur h en considerant (selon que l'on a choisit le coté AC) la base CB
on obtiens
.(t-AC).(t-BC)}}{BC})
avec
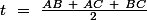
3)le segment de longueur
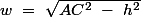
la valeur sinus de l'angle
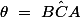
que l'on recherche est donc
 \ =\ \frac{h}{AC})
la valeur cosinus de l'angle
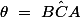
que l'on recherche est donc
 \ =\ \frac{w}{AC})
Passons à la valeur de l'angle
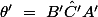
tout d'abord on construit le triangle rectangle formé par :
1)le coté AC (on aurait pu choisir aussi B'C'=BC+x mais bon aucune importance il faut choisir)
2)la hauteur h en considerant (selon que l'on a choisit le coté AC) la base C'B'=BC+x
on obtiens
.(t'-AC).(t'-BC-x)}}{BC+x})
avec
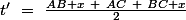
3)le segment de longueur
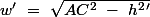
la valeur sinus de l'angle
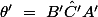
que l'on recherche est donc
 \ =\ \frac{h'}{AC})
la valeur cosinus de l'angle
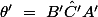
que l'on recherche est donc
 \ =\ \frac{w'}{AC})
alors à present passons à la valeur de l'angle
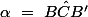
En admettant et on peut le faire que A=A' et C=C' ce qui a changé se sont les point B et B'
tout d'abord on construit le triangle rectangle formé par :
1)le coté BC
2)la hauteur


en considerant la base B'C'=BC+x du triangle BCB'
on obtiens
.(T_1-BB').(T_1-BC-x)}}{BC+x})
avec
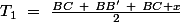
3)le segment de longueur
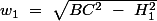
la valeur sinus de l'angle
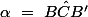
que l'on recherche est donc
 \ =\ \frac{H_1}{BC})
la valeur cosinus de l'angle
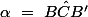
que l'on recherche est donc
 \ =\ \frac{w_1}{BC})
on doit tout d'abord determiner l'inconnue BB'
^2\ +\ H_1^2})
on obtiens
.(T_1-\sqr{(BC+x - w_1)^2\ +\ H_1^2}<br /><br />).(T_1-BC-x)}}{BC+x})
avec
^2\ +\ H_1^2}<br /><br />\ +\ BC+x}{2})
la valeur sinus de l'angle
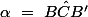
que l'on recherche est donc
 \ =\ \frac{H_1}{BC})
la valeur cosinus de l'angle
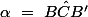
que l'on recherche est donc
 \ =\ \frac{w_1}{BC})
avec le systeme d'equation à résoudre:
.(\ T_1-\sqr{(BC+x - w_1)^2\ +\ H_1^2}<br /><br />\ ).(T_1-BC-x)}}{BC+x})
^2\ +\ H_1^2}}{2})