Déterminer tous les triplets de rationnels vérifiant :
Descente vers l'infini ... et au-delà !
18 messages
- Page 1 sur 1
déjà il faut voir que tu peux remplacer la question par "déterminer tous les triplets d'entiers tels que ....".
Ensuite, tu essayes de faire pareil que la déscente infinie pour montrer l'irrationalité de sqrt(2) :
un truc du genre si a+bsqrt(2) = 0, alors blablabla ..., a²-2b² = 0, donc a et b sont pairs et on peut remplacer a et b par a/2 et b/2
Ici, je doute pas qu'on puisse tenter un
si a+b*2^(1/3)+c*2^(2/3) = 0 alors blablabla ..., un bidule = 0, donc a,b, et c sont pairs etc.
Le truc consiste à trouver ce qu'on met dans le blablabla qui fasse la même chose dans les deux cas et qui donne un bidule qui marche.
Ensuite, tu essayes de faire pareil que la déscente infinie pour montrer l'irrationalité de sqrt(2) :
un truc du genre si a+bsqrt(2) = 0, alors blablabla ..., a²-2b² = 0, donc a et b sont pairs et on peut remplacer a et b par a/2 et b/2
Ici, je doute pas qu'on puisse tenter un
si a+b*2^(1/3)+c*2^(2/3) = 0 alors blablabla ..., un bidule = 0, donc a,b, et c sont pairs etc.
Le truc consiste à trouver ce qu'on met dans le blablabla qui fasse la même chose dans les deux cas et qui donne un bidule qui marche.
Merci doraki.
En fait jétais arrivé a une expression de ce genre (en remarquant que 2^{1/3} est la racine d'un certain trinôme) mais pour éliminer les racines il fallait élever au cube dans un 1er temps puis au carré alors j'ai vite laisser tomber (ce genre de calculs me découragent). J'ai pas encore essayé mais je voulais savoir s'il s'agissait de ta méthode.
En fait jétais arrivé a une expression de ce genre (en remarquant que 2^{1/3} est la racine d'un certain trinôme) mais pour éliminer les racines il fallait élever au cube dans un 1er temps puis au carré alors j'ai vite laisser tomber (ce genre de calculs me découragent). J'ai pas encore essayé mais je voulais savoir s'il s'agissait de ta méthode.
Salut,
Evidemment le titre est déjà un (gros) indice. Il faut (ou du moins, on peut) utiliser le principe de la descente infinie de Fermat (il n'existe pas de suite infinie strictement décroissante d'entiers positifs). Ici c'est vrai qu'on a affaire à des rationnels (en fait à des entiers comme l'a remarqué Doraki), mais il suffira de prendre la valeur absolue d'entiers bien choisis pour pouvoir l'utiliser ...
En ce qui concerne la méthode, la mienne est celle énoncée par Doraki
ce qui est dans le "bla bla" utilise une identité assez "classique" que j'ai d'ailleurs récemment mentionnée en aidant quelqu'un sur les polynômes à 3 variables ... :lol3:
Evidemment le titre est déjà un (gros) indice. Il faut (ou du moins, on peut) utiliser le principe de la descente infinie de Fermat (il n'existe pas de suite infinie strictement décroissante d'entiers positifs). Ici c'est vrai qu'on a affaire à des rationnels (en fait à des entiers comme l'a remarqué Doraki), mais il suffira de prendre la valeur absolue d'entiers bien choisis pour pouvoir l'utiliser ...
En ce qui concerne la méthode, la mienne est celle énoncée par Doraki
Ici, je doute pas qu'on puisse tenter un si a+b*2^(1/3)+c*2^(2/3) = 0 alors blablabla ..., un bidule = 0, donc a,b, et c sont pairs etc.
ce qui est dans le "bla bla" utilise une identité assez "classique" que j'ai d'ailleurs récemment mentionnée en aidant quelqu'un sur les polynômes à 3 variables ... :lol3:
Le but de ce qui est dans le blablabla est faire disparaître les termes en "2^1/3" du truc de gauche en le multipliant par un truc bien choisi, pour obtenir une relation dans Z, sur laquelle on sait mieux travailler.
Si tu élèves au cube, chuis pas sur que ça simplifie beaucoup les racines au final (d'ailleurs c'est pas exactement en élevant au carré le a+bsqrt(2) = 0 qu'on obtient a²-2b² = 0).
Si ta méthode donne une relation où les racines ont disparues, ben normalement tu devrais pouvoir continuer tranquillement avec.
Si tu élèves au cube, chuis pas sur que ça simplifie beaucoup les racines au final (d'ailleurs c'est pas exactement en élevant au carré le a+bsqrt(2) = 0 qu'on obtient a²-2b² = 0).
Si ta méthode donne une relation où les racines ont disparues, ben normalement tu devrais pouvoir continuer tranquillement avec.
Zweig tu fais comment pour trouver toutes ces relation ? Elle est très utile ici.
Sinon voila ce que j'ai fais:
Comme il a déjà été dis on peut se ramener a :
 avec a,b,c des entiers
avec a,b,c des entiers
On remarque alors que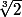 est une racine du trinôme
est une racine du trinôme 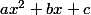 donc :
donc :
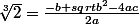 ou
ou 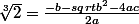
Cas 1: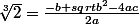
On élève au cube puis après simplification on tombe sur :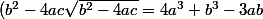
On élève au carre les 2 membres pour obtenir après simplification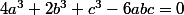
Il est assez facile de montrer alors que a, b et c sont paires et donc on peut trouver un nouvel triplet de solutions tel que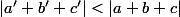 et donc on obtient une descente infinie.
et donc on obtient une descente infinie.
Après il me reste a traiter le cas ou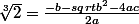 et la je me demande s'il n'y aurait pas un certain argument qui puisse me dispenser de traiter le 2eme cas. Est ce que c'est possible ?
et la je me demande s'il n'y aurait pas un certain argument qui puisse me dispenser de traiter le 2eme cas. Est ce que c'est possible ?
Aussi je voulais savoir si vous avez employé la descente infinie de la même manière que moi c-a-d en considérant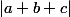 .
.
Sinon voila ce que j'ai fais:
Comme il a déjà été dis on peut se ramener a :
On remarque alors que
Cas 1:
On élève au cube puis après simplification on tombe sur :
On élève au carre les 2 membres pour obtenir après simplification
Il est assez facile de montrer alors que a, b et c sont paires et donc on peut trouver un nouvel triplet de solutions tel que
Après il me reste a traiter le cas ou
Aussi je voulais savoir si vous avez employé la descente infinie de la même manière que moi c-a-d en considérant
Salut,
Je comprend pas trop ce qu'attend Zweig comme réponse (une fois de plus...)
Si on a un tout petit bagage d'algèbre (bac+1), on sait que l'on peut faire de l'arithmétique sur K[X] pour tout corps K, en particulier pour Q[X] et, comme le polynôme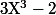 est irréductible dans Q[X] (car 1,-1,2,-2 ne sont pas racines) aucun polynôme non nul de degré <3 ne peut s'annuler en
est irréductible dans Q[X] (car 1,-1,2,-2 ne sont pas racines) aucun polynôme non nul de degré <3 ne peut s'annuler en 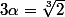 .
.
Si on veut le faire avec uniquement de l'arithmétique sur Z, on peut partir de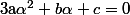 avec
avec 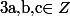 non tous nuls et premiers entre eux.
non tous nuls et premiers entre eux.
On peut alors multiplier par les deux "conjugués"^2+b(j\alpha)+c) et
et ^2+b(j^2\alpha)+c) où
où ) .
.
Cela revient en fait à multiplier par\alpha^2+(2a^2-bc)\alpha+(c^2-2ab)) et on obtient
et on obtient 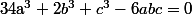
On en déduit alors en cascade que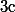 est pair puis que
est pair puis que 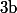 est pair puis que
est pair puis que  est pair ce qui contredit le fait que l'on avait supposé
est pair ce qui contredit le fait que l'on avait supposé 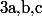 globalement premiers entre eux.
globalement premiers entre eux.
Je comprend pas trop ce qu'attend Zweig comme réponse (une fois de plus...)
Si on a un tout petit bagage d'algèbre (bac+1), on sait que l'on peut faire de l'arithmétique sur K[X] pour tout corps K, en particulier pour Q[X] et, comme le polynôme
Si on veut le faire avec uniquement de l'arithmétique sur Z, on peut partir de
On peut alors multiplier par les deux "conjugués"
Cela revient en fait à multiplier par
On en déduit alors en cascade que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tu multiplie 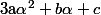 (qui vaut zéro) par
(qui vaut zéro) par ^2+b(j\alpha)+c) et par
et par ^2+b(j^2\alpha)+c) (qui sont deux nombres complexes)
(qui sont deux nombres complexes)
Si tu n'aime pas les complexes, tu multiplie directement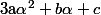 par
par \alpha^2+(2a^2-bc)\alpha+(c^2-2ab)) (qui lui est un réel)
(qui lui est un réel)
C'est texto la même chose que façe à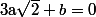 où tu multiplie par le conjugué
où tu multiplie par le conjugué 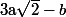 pour obtenir
pour obtenir 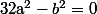
Si tu n'aime pas les complexes, tu multiplie directement
C'est texto la même chose que façe à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
oui : c'est l'un des trucs que l'on calcule lorsque l'on fait des extentions de corps (ici, l'énoncé se place dans Q[alpha])Qmath a écrit:Intéressant , j'aimerais bien savoir pourquoi "ça marche" , y -a-t-il toute une théorie derrière ?
Là où c'est pas super malin d'utiliser ça, c'est que cette notion n'est vue qu'au niveau L3 ou M1 alors que le fait que X^3-2 est irréductible sur Q[X] est trés élémentaire et permet de montrer le résultat demandé de façon bien plus simple...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
LeQmath a écrit:Juste par curiosité : le j viens du fait qu'on a affaire a un trinôme du second degrés ou bien de la presence d'une racine cubique qu'on cherche a éliminer ?
Quand je compare ma demo a celle de Zweig ou aux tiennes ... :mur: :ptdr:
Les trois racines (dans C) du polynôme
Cela signifie que les trois nombres
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut à vous deux,
Alors en fait, bah j'attendais rien, enfin j'voulais juste voir vos solutions. Finalement, on arrive tous à la même expression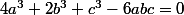 sur laquelle on fait des disjonctions de cas sur la parité des inconnues, la seule différence réside dans la manière d'y arriver, ta solution Ben étant la plus naturelle (j'avais même pas fait gaffe qu'on avait un polynôme du second degré ... En toute franchise, je n'aurai de toute façon pas pensé à multiplier par les "conjugués" même si c'est une technique classique, je me rappelle l'avoir vue l'année dernière quand on voulait démontrer des formules de combinatoire on utilisant les complexes).
sur laquelle on fait des disjonctions de cas sur la parité des inconnues, la seule différence réside dans la manière d'y arriver, ta solution Ben étant la plus naturelle (j'avais même pas fait gaffe qu'on avait un polynôme du second degré ... En toute franchise, je n'aurai de toute façon pas pensé à multiplier par les "conjugués" même si c'est une technique classique, je me rappelle l'avoir vue l'année dernière quand on voulait démontrer des formules de combinatoire on utilisant les complexes).
On arrive sinon directement au résultat en connaissant l'identité suivante :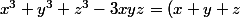(x^2 + y^2 + z^2 - xy - xz - yz))
On voit donc que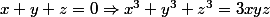
Alors en fait, bah j'attendais rien, enfin j'voulais juste voir vos solutions. Finalement, on arrive tous à la même expression
On arrive sinon directement au résultat en connaissant l'identité suivante :
On voit donc que
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
