Descente vers l'infini ... et au-delà (BIS)

[Zweig]

Yop,

Un exercice tombé à un oral d'Ulm. Aucune connaissance particulière en Arithmétique n'est exigée (hormis celle plus ou moins explicitée dans le titre ... :lol3:)

Soient des naturels fixés. Déterminer tous les -uplets d'entiers naturels vérifiant :

[CENTER][/CENTER]

[Anonyme]

On a combien de temps pour résoudre un tel exo lors d'un oral ?

[Zweig]

1h. Mais tu n'es pas tout seul, l'examinateur est aussi là pour t'aiguiller. Et encore heureux, les exos d'Ulm sont presque tous "infaisables" (bon à part pour le top 5 du classement ...). Et il ne faut pas avoir systématiquement 15 aux oraux de math pour être pris. Je connais des gens qui ont eu entre 5 et 7/20 à l'oral de math Ulm et qui ont été largement pris ... Bon après ils avaient géré les autres oraux/écrits aussi :lol3:.

En fait, cet exercice est loin d'être parachuté (pas comme d'autres exos d'Ulm). Déjà, on se convainc assez rapidement que l'unique n-uplet solution est celui nul. D'où l'idée de faire intervenir la descente infinie de Fermat (c'est pas systématique, mais quand on veut montrer qu'une équation diophantienne n'admet que la solution nulle, la descente aide généralement pas mal).

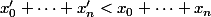
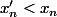
Comment appliquer d'une manière générale la descente ? On suppose qu'il existe un n-uplet solution qui ne coïncide pas avec le n-uplet nul et on montre qu'il existe un autre n-uplet solution tel que . En particulier, si on trouve un autre n-uplet solution avec , alors c'est suffisant. C'est ce qu'il va falloir faire ici ... Si je peux te donner un dernier indice : ce n'est pas un exercice d'arithmétique mais plutôt d'algèbre ... (bon, y a peut être d'autres manières de faire aussi).

[Ben314]

Bon, je me lance...

Si l'un des est nuls il sont tous nuls.
Supposons qu'il existe au moins une solution telle que et considérons en une telle que l'entier soit minimal.
Posons et ( si )
On a donc .
On a donc et, comme le trinôme admet deux racines et doit être à l'extérieur des racines.
Mais, si on avait alors on déduirait de que donc que puis que ce qui est absurde.
On a donc forcément donc

Mais, si on pose alors est racine de et la deuxième racine est entière (car ), strictement positive (car ) et strictement inférieure à (car )
Le n-uplet constitue une donc une nouvelle solution dont la somme des termes est strictement plus petite que... le minimum possible : absurde.

[Zweig]

Bravo :zen: :zen: