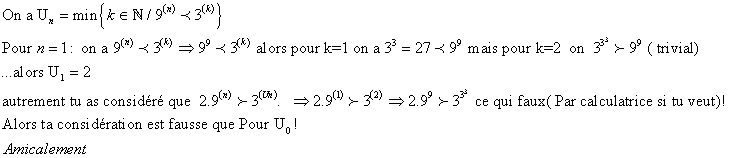Des tours de 9 et de 3
Olympiades mathématiques, énigmes et défis

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 16 Déc 2007, 00:10
par raito123 » 16 Déc 2007, 00:10
Bonne idée omar mais (
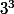^3)
est différent de

Les multiples ne doivent pas être utilisés sans nécessité
-
~oa~
- Membre Naturel
- Messages: 40
- Enregistré le: 02 Juil 2007, 18:38
-
 par ~oa~ » 16 Déc 2007, 00:15
par ~oa~ » 16 Déc 2007, 00:15
ah là vous avez raison ! (aviateur pilote et Raito) comme tu as dit raito et thsq j'ai confondus !!
l'essentiel c'est l'idée que j'essaierai de continuer avec.
A+
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Déc 2007, 00:19
par aviateurpilot » 16 Déc 2007, 00:19
mainteneat retour a ma solution incomplete
aviateurpilot a écrit:demostration qui n'est pas complete,
soit la suite
_{n\in\mathbb{N}})
tel que
}3^{2.3^{(U_n-1)}}>3^{(U_n+2)})
donc

donc

-
~oa~
- Membre Naturel
- Messages: 40
- Enregistré le: 02 Juil 2007, 18:38
-
 par ~oa~ » 16 Déc 2007, 00:38
par ~oa~ » 16 Déc 2007, 00:38
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Déc 2007, 00:53
par aviateurpilot » 16 Déc 2007, 00:53
attention,
}=9\neq 9^9)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Déc 2007, 01:01
par aviateurpilot » 16 Déc 2007, 01:01
de tt facon voila ce qui est sure
soit la suite
_{n\in\mathbb{N}})
tel que
}3^{2.3^{(U_n-1)}}>3^{(U_n+2)})
donc

donc

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités