Des drôles de gardiens
41 messages
- Page 1 sur 3 - 1, 2, 3
Des drôles de gardiens
Une petite énigme pour tous.
Tous les soirs, les gardiens d'une étrange prison effectuent un drôle de jeu.
Chaque gardien , avant de rentrer chez lui, va faire un tour des cellules, s'il en rencontre une ouverte, il la ferme, s'il en rencontre une fermée, il l'a rouvre.
Le premier gardien va effectuer le tour de toutes les cellules, le deuxième gardien ne va regarder qu'une cellule sur deux, le troisième qu'une cellule sur 3 etc... [on suppose qu'ils commencent tous à une cellule dite "0", donc le deuxième gardien visite en premier la 2ème cellule, et ne rencontrera donc pas la première, par exemple]
Si on considère qu'il y a n gardiens et m prisonniers (avec n <= m), et que les cellules sont initialement toutes fermées, comment peut-on savoir , après le passage de tous les gardiens, si le k-ième prisonnier pourra s'échapper?
Tous les soirs, les gardiens d'une étrange prison effectuent un drôle de jeu.
Chaque gardien , avant de rentrer chez lui, va faire un tour des cellules, s'il en rencontre une ouverte, il la ferme, s'il en rencontre une fermée, il l'a rouvre.
Le premier gardien va effectuer le tour de toutes les cellules, le deuxième gardien ne va regarder qu'une cellule sur deux, le troisième qu'une cellule sur 3 etc... [on suppose qu'ils commencent tous à une cellule dite "0", donc le deuxième gardien visite en premier la 2ème cellule, et ne rencontrera donc pas la première, par exemple]
Si on considère qu'il y a n gardiens et m prisonniers (avec n <= m), et que les cellules sont initialement toutes fermées, comment peut-on savoir , après le passage de tous les gardiens, si le k-ième prisonnier pourra s'échapper?
guillaumeL a écrit:Une petite énigme pour tous.
Tous les soirs, les gardiens d'une étrange prison effectuent un drôle de jeu.
Chaque gardien , avant de rentrer chez lui, va faire un tour des cellules, s'il en rencontre une ouverte, il la ferme, s'il en rencontre une fermée, il l'a rouvre.
Le premier gardien va effectuer le tour de toutes les cellules, le deuxième gardien ne va regarder qu'une cellule sur deux, le troisième qu'une cellule sur 3 etc... [on suppose qu'ils commencent tous à une cellule dite "0", donc le deuxième gardien visite en premier la 2ème cellule, et ne rencontrera donc pas la première, par exemple]
Si on considère qu'il y a n gardiens et m prisonniers (avec n <= m), et que les cellules sont initialement toutes fermées, comment peut-on savoir , après le passage de tous les gardiens, si le k-ième prisonnier pourra s'échapper?
J'ai pas très bien compris le problème car si le premier gardien ouvre toutes les cellules fermées, alors TOUS les prisionniers s'échapperont dès le passage du premier gardien. :hein:
guillaumeL a écrit:Une petite énigme pour tous.
Tous les soirs, les gardiens d'une étrange prison effectuent un drôle de jeu.
Chaque gardien , avant de rentrer chez lui, va faire un tour des cellules, s'il en rencontre une ouverte, il la ferme, s'il en rencontre une fermée, il l'a rouvre.
Le premier gardien va effectuer le tour de toutes les cellules, le deuxième gardien ne va regarder qu'une cellule sur deux, le troisième qu'une cellule sur 3 etc... [on suppose qu'ils commencent tous à une cellule dite "0", donc le deuxième gardien visite en premier la 2ème cellule, et ne rencontrera donc pas la première, par exemple]
Si on considère qu'il y a n gardiens et m prisonniers (avec n <= m), et que les cellules sont initialement toutes fermées, comment peut-on savoir , après le passage de tous les gardiens, si le k-ième prisonnier pourra s'échapper?
Non, c'est que j'ai bien lu... Le premier gardien ouvre toutes les cellules (initialement fermées) et tous les prisionniers s'évadent.
Non, c'est que j'ai bien lu... Le premier gardien ouvre toutes les cellules (initialement fermées) et tous les prisionniers s'évadent.
Non! Ils attendent que tous les gardiens soient passés avant d'essayer de fuir (c'est vraiment de bon prisonnier quand même )! Par exemple, le premier gardien ouvre la deuxième cellule, certes, mais le deuxième gardien va refermer cette même cellule, tu vois? Donc le 2ème prisonnier ne partira pas, sauf si il n'y a qu'un gardien. [si ça te choques que les prisonnier ne s'évadent pas directement lorsqu'on ouvre une cellule, remplace la question par : est-ce que la k-ième porte sera ouverte ou fermée après le passage de tous les gardiens :id: ]
Zut, j'ai dis une bêtise:
Le premier prisonnier est certain de sortir
Le deuxième est certain de rester
Le troisième est certain de sortir...
Je prends une mauvaise direction ?
S'il y a au moins un gardien, le premier prisonnier est en effet certain de sortir. Pour le deuxième, ça dépend, si n = 1, il pourra sortir, si n >= 2 , il ne pourra pas. etc... il faut essayer de chercher une méthode pour le cas général
guillaumeL a écrit:Non! Ils attendent que tous les gardiens soient passés avant d'essayer de fuir! Par exemple, le premier gardien ouvre la deuxième cellule, certes, mais le deuxième gardien va refermer cette même cellule, tu vois? Donc le 2ème prisonnier ne partira pas, sauf si il n'y a qu'un gardien. [si ça te choques que les prisonnier ne s'évadent pas directement lorsqu'on ouvre une cellule, remplace la question par : est-ce que la k-ième porte sera ouverte ou fermée après le passage de tous les gardiens :id: )
S'il y a au moins un gardien, le premier prisonnier est en effet certain de sortir. Pour le deuxième, ça dépend, si n = 1, il pourra sortir, si n >= 2 , il ne pourra pas. etc... il faut essayer de chercher une méthode pour le cas général
Ok ! Je viens de cadrer le problème. On suppose aussi qu'il y a
LEFAB11 a écrit:Oui c'est vrai j'ai supposé qu'il y avait autant de prisonniers que de gardiens. :mur:
Parce que bon, j'ai pas envie de faire mon Flodelarab, mais si il y a
Verdict ?
Clembou a écrit:Parce que bon, j'ai pas envie de faire mon Flodelarab, mais si il y acellules pour
prisonniers (
) on peut imaginer un placement pour les prisionniers. Donc la première cellule est ouverte mais si elle est vide, il n'y a aucun prisionnier qui sort.
Verdict ?
Cela va devenir tendu tout ça!! :bad3:
Faut que tu revois ta conjugaison du futur de décomposer :ptdr:
Et tu ne réponds pas à ma question. Pourquoi tu décomposeras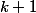 en ses facteurs premiers ?
en ses facteurs premiers ?
PS : C'est bien ! Tu admets que tu viens de faire une erreur de conjugaison. Au lieu de me traiter de "triple buse", relis toi et aies conscience que tu n'as pas toujours raison.
PS2 : Je crois que j'ai résolu l'énigme. :++:
http://www.la-conjugaison.fr/du/verbe/decomposer.php a écrit:Futur simple
je décomposerai
tu décomposeras
il décomposera
nous décomposerons
vous décomposerez
ils décomposeront
Et tu ne réponds pas à ma question. Pourquoi tu décomposeras
PS : C'est bien ! Tu admets que tu viens de faire une erreur de conjugaison. Au lieu de me traiter de "triple buse", relis toi et aies conscience que tu n'as pas toujours raison.
PS2 : Je crois que j'ai résolu l'énigme. :++:
41 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
