Densité sur [0, 1]
Olympiades mathématiques, énigmes et défis
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 27 Juin 2010, 15:22
par Zweig » 27 Juin 2010, 15:22
Salut,
On considère la suite
)
, avec

.
Montrer que les valeurs de la suite sont denses dans

.
On montre aussi que cette suite est équidistribuée sur  , i.e, si on choisit
, i.e, si on choisit  et que l'on note
et que l'on note) le nombre de termes
le nombre de termes 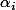 ,
, 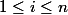 , qui se trouvent dans
, qui se trouvent dans 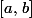 , alors
, alors[CENTER]
}{n}=b-a)
[/CENTER]
Voir le critère de Weyl :
http://moduloserge.free.fr/HX1-05/DM/dm15%28Weyl%29.pdf
-
Finrod
- Membre Irrationnel
- Messages: 1944
- Enregistré le: 24 Sep 2009, 10:00
-
 par Finrod » 27 Juin 2010, 19:52
par Finrod » 27 Juin 2010, 19:52
Il me semble avoir vu passé la question sur le forum déjà mais je n'ai pas le courage de retrouver ça.
C'est une sous-groupe de R modulo 1, donc à priori c'est soit discret soit dense. En supposant un minimum par l'absurde, on doit le trouver dense.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 27 Juin 2010, 23:58
par Nightmare » 27 Juin 2010, 23:58
Salut,
tu peux montrer que l'équirépartition de la suite est équivalent au fait que pour toute fonction continue f,
\longrightarrow_{n\infty} \Bigint_{0}^{1} f)
(Disons qu'on l'admet provisoirement parce que ... je n'arrive plus à le démontrer :euh:)
Ceci dit, il suffit donc de montrer que pour toute fonction continue f,
)\longrightarrow_{n\infty} \Bigint_{0}^{1} f)
Ca marche par étape : Vrai pour les polynômes trigonométriques (vérifier en posant

). Vrai du coup par densité pour toutes les fonctions continues prenant la même valeur en 0 et en 1. Reste à généraliser à toutes les fonctions continues, suffit des les approcher correctement par des fonctions qui prennent la même valeur en 0 et 1. Je te laisse mettre ça au propre.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Juin 2010, 09:29
par Doraki » 28 Juin 2010, 09:29
J'dirais plutot que pour toute fonction f continue et 1-périodique,
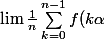 = \int_0^1 f)
comme ça on s'embête pas avec la partie entière.
si
 = e^{2i \pi p x})
ça fait
} = 0)
donc ça marche.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités