Voilà un exercice assez interessant d'algèbre :
Première Partie :
1/Construiser une bijection entre N et pN / p entier naturel strictement supérieur à 0 .
Quel conditions doit on prendre sur p pour q'il existe une bijection
2/ Construiser une bijection entre N et Z .
3/ Peut on construire une bijection entre N et Q ? Conclure
4/Montrer qu'il n'existe pas d'application bijective de N vers un intervalle fermé de R . Généraliser ensuite à R
Deuxieme Partie :
Soit la relation binaire definie sur un ensemble E , les sous ensembles Fi
card(F1)< card (F2)
Montrer que c'est une relation d'ordre , est elle totale ?
Donner l'ensembles des majorants , des minorants
Dénombrement des Ensembles Infini
3 messages
- Page 1 sur 1
bref construire les bijection que tu demande n'est vraiment pas difficile, en donner des expressions formelles est beacoup plus dure par contre :
as tu pensé tout simplement à = p*n)
une condition sur p? j'en ai pas vue mais bon tu peut te contraindre à n'utiliser que les p que tu veut.
bon la c'est plus amusant, tu peut vérifier qu'en sautant alternativement autour de 0 et en s'eloignant au fur à mesure tu va parcourir tout les Z, c'est la bijection que tu cherche. Elle s'exprime assez simplement :
=0)
=n)
=-n)
c'est pas la seule bien évidemment
la réponse est oui, mais donner une expression de cette bijection n'est pas du tout evidente. Par contre on peut assez aisement donner une injection de Q dans N. en faite il vaut mieux d'abors montrer qu'il y a une injection de Q dans N². Puis une de N² dans N. vue qu'il y a une injection Q est donc denombrable.
A titre d'indication la bijection la plus simple de N² dans N, c'est le parcourt des diagonales successif. Bon juste pour le fun en voila une expression :
=\frac{1}{2}(n+m)(n+m+1)+n)
A enfin quelque chose de plus amusant, en faite ceci a ete demontrez par peano, à qui on doit des beaux travaux sur les transfinis, il a été le premier à proposer une classification des ensembles infinis, par leur cardinal.
pour R on montre qu'il n'est pas dénombrable en procédant par l'absurde. Tu suppose donc que t'a un dénombrement de tout les réel entre 0 et 1 :
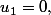


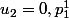


.
.
.
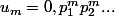
 ...
...
on peut alors construire un autre réel, tel que
tel que  , donc ce dernier n'apparait pas dans le dénombrement. ce qui est absurbe.
, donc ce dernier n'apparait pas dans le dénombrement. ce qui est absurbe.
Zeryeb a écrit:1/Construiser une bijection entre N et pN / p entier naturel strictement supérieur à 0
as tu pensé tout simplement à
une condition sur p? j'en ai pas vue mais bon tu peut te contraindre à n'utiliser que les p que tu veut.
Zeryeb a écrit:2/ Construiser une bijection entre N et Z
bon la c'est plus amusant, tu peut vérifier qu'en sautant alternativement autour de 0 et en s'eloignant au fur à mesure tu va parcourir tout les Z, c'est la bijection que tu cherche. Elle s'exprime assez simplement :
c'est pas la seule bien évidemment
Zeryeb a écrit:3/ Peut on construire une bijection entre N et Q ? Conclure
la réponse est oui, mais donner une expression de cette bijection n'est pas du tout evidente. Par contre on peut assez aisement donner une injection de Q dans N. en faite il vaut mieux d'abors montrer qu'il y a une injection de Q dans N². Puis une de N² dans N. vue qu'il y a une injection Q est donc denombrable.
A titre d'indication la bijection la plus simple de N² dans N, c'est le parcourt des diagonales successif. Bon juste pour le fun en voila une expression :
Zeryeb a écrit:4/Montrer qu'il n'existe pas d'application bijective de N vers un intervalle fermé de R . Généraliser ensuite à R
A enfin quelque chose de plus amusant, en faite ceci a ete demontrez par peano, à qui on doit des beaux travaux sur les transfinis, il a été le premier à proposer une classification des ensembles infinis, par leur cardinal.
pour R on montre qu'il n'est pas dénombrable en procédant par l'absurde. Tu suppose donc que t'a un dénombrement de tout les réel entre 0 et 1 :
.
.
.
on peut alors construire un autre réel,
De l'histoire des alephs ...
justes quelques remarques pour approfondir eventuellement le sujet : tous ces travaux sur les bijections entre ensembles infinis ont occupés toute la vie de Cantor ; le fait qu'il n'y ait pas de bijection possible entre Q et R a amené à définir plusieurs " infinis " , idée non naturelle pourtant , le plus petit étant N ( infini de type " aleph 0 " ) et de même taille que Z ou Q , puis viens R ( " aleph 1 " ) . Et le plus étonnant : R^2 a le mème cardinal que R ainsi que R^3... et R^infini ! Tout ceci nous amène à une conclusion bien étrange : il y a autant de points a l'intèrieur d'un carré que de points sur un des cotês de ce même carré ! Et il y a autant de points sur un segment de un milimètre de long que dans une hypersphère de 10 kilomètres de diamètre ! Si on note An " aleph n " on a des propriétés du type :
(An)^P = An ( pour tout p entier naturel même infini ... )
2^(An)= A(n+1) ( R a le même cardinal que l'ensemble des parties de N )
Construire des alephs de plus en plus grands est alors tout à fait possible ( prendre l'ensemble des parties de l'ensemble considéré ) mais leur interprétation devient plus difficile:
si " aleph 0 " et aleph 1 " s'interprètent assez facilement ( alpeh 1 : l'ensemble des points d'une droite ) ; pour des " alephs " plus grands l'interprétation devient plus dure , la taille des ensembles augmentant de façon colossalle avec les alephs : aleph 2 correspond a l'ensemble des courbes géométriques ( par exemple ) ; pour aleph 3 , aucune interprétation n'existe encore ...
Une question interessante que l'on peut se poser : quel est " l'aleph " de l'ensemble des fonctions réelles ? ( fonctions de R dans R , telles que :
x -> ( 1/x ) , x-> cosx ... sachant que celles-ci ne représentent qu'une " goutte d'eau dans l'océan des fonctions réelles " , tout comme l'ensemble des fonctions continues ... ).
On peut déjà noter que son " aleph " est plus grand que 2 : en effet il existe une application injective de 2^R ( ensemble des parties de R ; aleph 2 ) dans l'ensemble considéré que l'on notera F : à une partie de R on associe la fonction f de F définie par : f(x)=x si x est dans la partie de R considérée et 0 sinon ; la fonction nulle serait alors celle correspondant à la partie vide de R ; la fonction x -> x sur R correspond au cas ou la partie considérée est R tout entier ...
On note par contre que cette application est " loin " d'être surjective : on obtient en effet qu'une part " insignifiante " de F ( on est loin de reconstituer tous les cosx , sinx , x^2 ..... ).
F est donc de cardinal supèrieur à aleph 2 .
Tiendrai-t-on un exemple d'aleph 3 ?
(An)^P = An ( pour tout p entier naturel même infini ... )
2^(An)= A(n+1) ( R a le même cardinal que l'ensemble des parties de N )
Construire des alephs de plus en plus grands est alors tout à fait possible ( prendre l'ensemble des parties de l'ensemble considéré ) mais leur interprétation devient plus difficile:
si " aleph 0 " et aleph 1 " s'interprètent assez facilement ( alpeh 1 : l'ensemble des points d'une droite ) ; pour des " alephs " plus grands l'interprétation devient plus dure , la taille des ensembles augmentant de façon colossalle avec les alephs : aleph 2 correspond a l'ensemble des courbes géométriques ( par exemple ) ; pour aleph 3 , aucune interprétation n'existe encore ...
Une question interessante que l'on peut se poser : quel est " l'aleph " de l'ensemble des fonctions réelles ? ( fonctions de R dans R , telles que :
x -> ( 1/x ) , x-> cosx ... sachant que celles-ci ne représentent qu'une " goutte d'eau dans l'océan des fonctions réelles " , tout comme l'ensemble des fonctions continues ... ).
On peut déjà noter que son " aleph " est plus grand que 2 : en effet il existe une application injective de 2^R ( ensemble des parties de R ; aleph 2 ) dans l'ensemble considéré que l'on notera F : à une partie de R on associe la fonction f de F définie par : f(x)=x si x est dans la partie de R considérée et 0 sinon ; la fonction nulle serait alors celle correspondant à la partie vide de R ; la fonction x -> x sur R correspond au cas ou la partie considérée est R tout entier ...
On note par contre que cette application est " loin " d'être surjective : on obtient en effet qu'une part " insignifiante " de F ( on est loin de reconstituer tous les cosx , sinx , x^2 ..... ).
F est donc de cardinal supèrieur à aleph 2 .
Tiendrai-t-on un exemple d'aleph 3 ?
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
