La démonstration élémentaire du dernier théorème de Fermat
curiosul a écrit:x, y, z ne sont pas les memes solutions comme les solutions d'ecuation ou j'ai remplace la valeur n=1.
Ce qui se respect toujour est la valeur de n.
Je veux dire que l'ecuation
n'est pas la meme comme l'ecuation
Ce qui ne se change pas sont les valeurs x, y, z sans l'exposant et la valeur de n dans l'ecuation
Nous pouvons également trouver d'autres moyens pour montrer que

sont les seules solutions du système

Si les deux égalités du dernier système sont vrais simultanément dans un triangle, on peut aussi écrire les égalités :
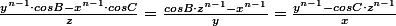
et aussi
^n=\left (\frac{cosB\cdot z^{n-1}-x^{n-1}}{y} \right )^n=\left (\frac{y^{n-1}-cosC\cdot z^{n-1}}{x} \right )^n)
et également
^n=\left (\frac{cosB\cdot z^{n-1}-x^{n-1}}{y} \right )^n+\left (\frac{y^{n-1}-cosC\cdot z^{n-1}}{x} \right )^n)
^n=\frac{z^n}{2y^n} \left (cosB\cdot z^{n-1}-x^{n-1} \right )^n+\frac{z^n}{2x^n}\left (y^{n-1}-cosC\cdot z^{n-1} \right )^n)
Mais nous avons montré que si les égalités du système sont vraies :

et également, si on considere

nous arrivons à l'égalité
^n= \left (cosB\cdot z^{n-1}-x^{n-1} \right )^n+\left (y^{n-1}-cosC\cdot z^{n-1} \right )^n)
Donc, nous pouvons conclure que si les égalités du système

sont simultanément vraies, alors on obtient les égalités:
^n= \left (cosB\cdot z^{n-1}-x^{n-1} \right )^n+\left (y^{n-1}-cosC\cdot z^{n-1} \right )^n \\ <br /> \left (y^{n-1}\cdot cosB-x^{n-1}\cdot cosC \right )^n=\frac{z^n}{2y^n} \left (cosB\cdot z^{n-1}-x^{n-1} \right )^n+\frac{z^n}{2x^n}\left (y^{n-1}-cosC\cdot z^{n-1} \right )^n <br />\end{cases})
Nous pouvons affirmer que si z > y > x > 0, alors les égalités du système ci-dessus sont tous les deux vraie seulement si
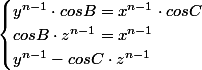
Nous avons montré dans le premier post que si

Pour n > 2, entre les côtés x, y, z, considérés des entiers z > y > x , il n'y a pas égalité:
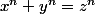
Et il suffit de démontrer le grand théorème de Fermat.
sont les seules solutions du système
Si les deux égalités du dernier système sont vrais simultanément dans un triangle, on peut aussi écrire les égalités :
et aussi
et également
Mais nous avons montré que si les égalités du système sont vraies :
et également, si on considere
nous arrivons à l'égalité
Donc, nous pouvons conclure que si les égalités du système
sont simultanément vraies, alors on obtient les égalités:
Nous pouvons affirmer que si z > y > x > 0, alors les égalités du système ci-dessus sont tous les deux vraie seulement si
Nous avons montré dans le premier post que si
Pour n > 2, entre les côtés x, y, z, considérés des entiers z > y > x , il n'y a pas égalité:
Et il suffit de démontrer le grand théorème de Fermat.
adrien69 a écrit:Alors, c'est égal ou bien c'est différent ?
Adrien Bonjour!
Je comprends ce que vous voulez dire.
Le message précédent est juste une autre analise dans le cas quand on considere les solution inégale.
S'il vous plaît, lire le premier message dans cette discussion, pour comprendre ce que je veux dire.
J'ai essayé d'aller avec la supposition que les solutions ne sont pas egales et nous avons conclu qu'ils sont en fait égales.
Ce ca que j'ai pensé.
leon1789 a écrit:Dans votre preuve, où utilisez-vous une propriété arithmétique sur les entiers x,y,z ?
Bonjour Leon!
Je ne sais pas exactement comment vous répondre.
Mais je dirais que j'ai utilisé les valeurs numériques des côtés du triangle, en tant que propriétés arithmétiques sur les entiers x,y,z.
curiosul a écrit:Bonjour Leon!
Je ne sais pas exactement comment vous répondre.
Mais je dirais que j'ai utilisé les valeurs numériques des côtés du triangle, en tant que propriétés arithmétiques sur les entiers x,y,z.
Je pense qu'il te demandait quels théorèmes de natures arithmétiques tu avais utilisés pour démontrer le résultat.
adrien69 a écrit:Je pense qu'il te demandait quels théorèmes de natures arithmétiques tu avais utilisés pour démontrer le résultat.
Bonjour Adrien!
Même si sa question n'était pas cela, on peut considérer cela comme votre question.
J'ai essayé d'utiliser les opérations arithmétiques les plus communes et triviales.
Je ne pense pas avoir utilisé un théorème, sauf le théorème de cosinus.
C'est vrai qu'on peut considérer cela comme un domaine de la géométrie,
mais si toute courbe elliptique est modulaire, c'est aussi un domaine de la géométrie, n'est ce pas ?
De même, je pense que nous pouvons adapter la logique d'un problème à un autre domaine de la mathématique pour le résoudre.
Il est possible toutefois que ce type de raisonnement n'est pas valable?
Je regarde rapidement la preuve et me rends compte que pour montrer
que "Pour n>2, l'équation* x^n+y^n=z^n n'a pas de solutions dans N."
tu arrives à
donc pour montrer "A" il suffit de montrer "A"...
que "Pour n>2, l'équation* x^n+y^n=z^n n'a pas de solutions dans N."
tu arrives à
Mais il suffit de montrer que :
"Pour n>2, l'équation* x^n+y^n=z^n n'a pas des solutions entiers."
donc pour montrer "A" il suffit de montrer "A"...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Sylviel a écrit:Je regarde rapidement la preuve et me rends compte que pour montrer
que "Pour n>2, l'équation* x^n+y^n=z^n n'a pas de solutions dans N."
tu arrives à
donc pour montrer "A" il suffit de montrer "A"...
Bonjour Sylviel!
Ce que je veux dire, c'est:
Si l'on considère x, y, z, les côtés d'un triangle, des valeurs entiers naturelles z> y> x,
nous avons montré que pour n> 2, entre les côtés x, y, z du triangle, il n'y a pas l'égalité
"A"...
Parce que les solutions x, y, z peuvent être considérés comme les côtés d'un triangle, des nombres entiers positifs z> y> x, est équivalente avec l'affirmation du l'enonce du grand théorème de Fermat.
Donc, bien qu'il puisse sembler dépacé, oui,
pour montrer "A" il suffit de montrer "A"..
et nous avons montré "A",
mais par rapport à des côtés d'un triangle, non directemment .
Mais nous avons montré la même chose... "A".
Excusez-moi si je répondu à votre question d'une manière qui n'est pas évident d'où il vient "l'incohérente de la logique".
Mais même si les valeurs de x, y, z appartiennent à N, on peut étendre à Z.
Supposer a, b;);), c de façon que l'égalité suivante est vraie :
donc, aussi
et dans ce cas on considère les valeurs entières positives, a, b(/-b), c les côtés du triangle et dans ce cas a > b > c, ou a > c > b.
adrien69 a écrit:Curiosul, Dacu, c'est quoi votre langue natale ? On comprendrait peut-être un peu plus ce que vous écrivez dans la preuve.
C'est vraiment sans méchanceté aucune. Juste que je ne comprends pas toujours ni parfaitement ce que vous dites.
Pour l'instant, sont des raisons que je ne peux pas vous le dire.
Quoi qu'il en soit, je comprends bien ce que vous dites et pour l'instant, même si je ne suis pas en mesure de répondre ainsi que vous pouvez comprendre, je n'ai pas reçu un contre-argument évident qui doit être accepté pour la validité de cette démonstration.
C'est dommage que nous ne pouvons pas bien comprendre.
Mon but n'est pas de vous convaincre de l'exactitude de cette démonstration, mais pour me convaincre moi-même si il y a une erreur évident.
Qu'est-ce que vous m'avez dit jusqu'à présent n'est pas, bien qu'elle puisse aussi être une tell erreur.
curiosul a écrit:Bonjour Adrien!
Même si sa question n'était pas cela, on peut considérer cela comme votre question.
J'ai essayé d'utiliser les opérations arithmétiques les plus communes et triviales.
Je ne pense pas avoir utilisé un théorème, sauf le théorème de cosinus.
C'est vrai qu'on peut considérer cela comme un domaine de la géométrie,
mais si toute courbe elliptique est modulaire, c'est aussi un domaine de la géométrie, n'est ce pas ?
De même, je pense que nous pouvons adapter la logique d'un problème à un autre domaine de la mathématique pour le résoudre.
Il est possible toutefois que ce type de raisonnement n'est pas valable?
Je demande quel(s) théorème(s) arithmétique(s) vous utilisez (je ne parle pas des opérations + - * /).
Apparemment aucun, c'est fort... (les relations entre longueurs des cotés et angles d'un triangle ne sont pas de l'arihmétique !).
Donc je précise ma question : où utilisez-vous spécifiquement que x,y,z sont des entiers ?
leon1789 a écrit:Donc je précise ma question : où utilisez-vous spécifiquement que x,y,z sont des entiers ?
Au début, par exemple:
curiosul a écrit:Les solutions de l'équationpeuvent être considérée les côtés x, y, z d'un triangle, de même aussi, les valeurs x, y, z, peuvent être considéré comme des entiers z > y > x, des côtés valeurs entiers d'un triangle, car dans les deux cas, la solution z vérifie l'inégalité y+x > z > y.
Bien sûr, l'expression n'est pas correcte en français, mais il peut être compris pour ceux qui veulent comprendre ce que je veux dire.
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
