curiosul a écrit:"Pour n>2, l'équation*
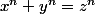
n'a pas des solutions entiers."
Demonstration:Les solutions de l'équation peut être considérée les côtés x, y, z d'un triangle, z > y > x, car dans les deux cas, la solution z vérifie l'inégalité y+x > z > y.
Si on considère de vrai l'égalité
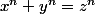
entre les côtés x, y, z d'un triangle, on peut former le système:
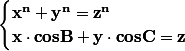
où les angles B et C sont les angles formés par les côtés x et z, respectivement y et z, et aussi:
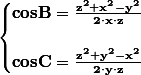
Si les deux égalités sont vraies dans un triangle, alors nous pouvons écrire l'équation:
z^{n-1}})
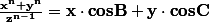
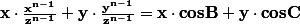
Donc, les deux égalités*du système initial sont vrais si
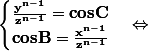
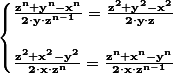
Si les deux égalités ci-dessus sont vrais, l'égalité suivante doit être aussi vrai:
})
Pour n = 2, l'égalité est vraie.
Pour les valeurs entières de n supérieur à 2,
l'égalité ci-dessus n'est pas possible si z> y> x.
Le cas 1. n=3 })
=(y^3+x^3)(y^2-x^2)})
(y^2+xy+x^2)=(y^3+x^3)(y-x)(y+x)})
=(y^3+x^3)(y+x)})
=z(y^3+x^3)(y+x)})
(y^2+xy+x^2)=z(y^3+x^3)(y+x)})
})
=z(y+x)})
(z-x)})
(z-x)})
=y(y+x)(z-x)})
(z^2+zx+x^2)=y(y+x)(z-x)})
})
+x^2=y(y+x)})
Parce que z > y > x cela veut dire que
>y(y+x)\Rightarrow z(z+x)+x^2>y(y+x)})
Donc, pour le cas n = 3 :
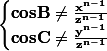
Cela est en contradiction avec une d'entre les deux relations du système
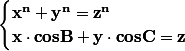
Mais parce que la seconde relation est vraie dans tout triangle, signifie que pour n = 3, la premiere relation du système n'est pas vrai.
Le cas 2. n>3 =z^n(y^2-x^2)})
=(x^n+y^n)(y^2-x^2)})
(y^{n-1}+y^{n-2}x+...+yx^{n-2}+x^{n-1})=(x^n+y^n)(y-x)(y+x)})
=yx^n+x^{n+1}+y^{n+1}+xy^n})
En comparant les termes nous remarquons que si z> y> x, alors:
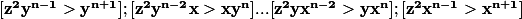
ainsi, également pour n> 3
})
donc, pour le cas n> 3 aussi, il s'ensuit que:
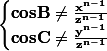
ce qui contredit l'une des égalités
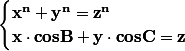
Donc, pour n entier supérieur à 2, entre les côtés x, y, z d'un triangle, z>y>x , il n'y a pas l'égalité
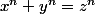
, sauf si
, mais dans ce cas, z n'est pas un nombre entier.
Mais il suffit de montrer que :
"Pour n>2, l'équation*
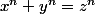
n'a pas des solutions entiers."
;)la démonstration. Ne doit pas supposer qu'il ne peut pas exister aucune telle démonstration.