Deja posté par Zebelon

[aviateurpilot]

je je vai recomencer et correcter tous les fautes que j'ai fait:
A:1saut d'une marche
B:1saut de 2 marches
soit E={tt les combinaisons possible}
={les combinaisons començant par "A"}
={les combinaisons començant par "BA"}
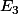
={les combinaisons començant par "BBA"}
il est clair que les combinaisons començant par "BBA" et totalement differente des combinaisons començant par "BA"
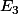
dans la 2eme action c'est "A" mais dans la 2eme action c'est "B"
donc ce que t'a dit est faux :

car

il est meme clair que
et

=> dans il a fait "A" et il lui rest n-1 marches dont le nombre de possibilité est
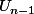
=> dans il a fait "BA" et il lui rest n-3 marches dont le nombre de possibilité est
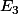
=> dans il a fait "BBA" et il lui rest n-5 marches dont le nombre de possibilité est

et puisque
et
alors:


stp BANCH donne moi un raisonement mathématique pour chaque faute que tu remarque. je vai aller manger queque chose et je revien :++:

[BancH]

Oui ça à l'air bon sauf que tu as oublié quelque chose:


Les crampes !!

Tu n'as comptabilisé que les crampes dûes aux 4 premiers sauts.

Je pense que ma formule est bonne:

avec le quotient de la division euclidienne de par :

[aviateurpilot]

dans moi alors un debut d'une combinaison qui ne comence ni par "A" ni "BA"
ni "BBA" ........?

[BancH]

dans moi alors un debut d'une combinaison qui ne comence ni par "A" ni "BA"
ni "BBA" ........?

Je ne comprends pas ce que tu veux dire.

Ta formule à toi admet la combinaisons suivante:

aaaaaaab-ab-aaab-aaab-b-aab-b-b-b-b-b-b-b-b-b-b-b-b-b-b-b-b-b-b-b-

Donc elle est fausse.

[aviateurpilot]

mais quand j'ai dit ={le nombre de combinaisons començent par "A"} je parle seulement des combinaisons possibles

[BancH]

Ah oui, ta formule semble fonctionner, je pensais qu'elle était fausse à cause d'un erreur de calcul.

[aviateurpilot]

ok :zen:
mais cette methode là est basée sur ta methode
j'ai utilisé ta remarque en travaillant par le debut des combinaisons
c'est plus facile que travailler par la fin des combinaisons

mais il ne reste à calculer le nombre de possibilités en fonction de n

[BancH]

En développant peut-être.

[aviateurpilot]

oui c ce que j'ai dit

maintenant on doit calculer en fonction de n

[hero_h_2zef]

salu tt le monde : la réponse à la première énigme est : 1 + (n-1) + C(2,(n-1)) + C(3,(n-1))
+.... + C( [ (n + 1) / 3 ] , (n-1) ) .
La grenouille peut en effet sauter 0 fois deux marches ou 1 fois deux marches ( elle a alors (n-1) marches possibles pour ce faire , étant donné qu'elle ne peut pas sauter deux marches sur l'avant dernière marche ou sur la dernière mais sur
la 0 ème on peut ) ou 2 fois deux marches ... jusqu'au nombre total de " doubles sauts " possibles c'est-à-dire [ (n + 1) /3 ] : on le montre en effet par récurrence en ininisialisant pour n = 2 ( on bien un saut de deux marches possible ) et en remarquant que ce nombre augmente tous les trois escaliers .