Deja posté par Zebelon
Olympiades mathématiques, énigmes et défis
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 00:23
par BancH » 16 Juin 2006, 00:23
Voilà, j'ai une solution,mais ma démonstration est peut-être mal expliquée:
Un saut d'une marche est noté a, un saut de deux marches est noté b- deux sauts de deux marches suivis d'un saut d'une marche (dû aux crampes du crapaud) sont notés b-b-a
Les combinaisons de sauts sont:avec n=1:a
=> 1 combinaisonavec n=2:On prend les combinaisons de n=2-1, auxquelles on ajoute a devant.aa
On remplace les aa commençant une combinaison par b- si aa n'est pas suivi de b-b-b-
=> 2 combinaisons
avec n=3:On prend les combinaisons de n=3-1, auxquelles on ajoute a devant.aaa
ab-
On remplace les aa commençant une combinaison par b- si aa n'est pas suivi de b-b-b-a
=> 3 combinaisonsavec n=4:aaaa
aab-
ab-a
b-aa
b-b-
=> 5 combinaisons
avec n=5:aaaaa
aaab-
aab-a
ab-aa
ab-b-
b-aaa
b-ab-
b-b-a
=> 8 combinaisonsavec n=6:aaaaaa
aaaab-
aaab-a
aab-aa
aab-b-
ab-aaa
ab-ab-
ab-b-a
b-aaaa
b-aab-
b-ab-a
b-b-aa
=> 12 combinaisons
A chaque fois que n augmente de 1, on prend:n combinaisons
+ le nombre de combinaisons de n marches commençant par a qui est donc égal au nombre de combinaisons de

marches
- le nombre de combinaisons de n marches commençant par ab-b-, soit 1 pour tout
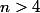
.
Avec

le nombre de combinaisons avec n marches et
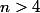
, on a donc:

Et pour n<4:
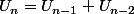
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 00:49
par aviateurpilot » 16 Juin 2006, 00:49
=>le nombre de combinaisons de n marches commençant par a qui est égal au nombre de combinaisons de n-1 marches
=> le nombre de combinaisons començant par "ba" est
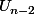
et puisque on n'a pas calculé le nombre de combinaisons començant par "bb"
alors normalement

mais ta formule ne verifie pas ça
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:06
par aviateurpilot » 16 Juin 2006, 01:06
n>4
il y a 3 possibilités
la combinaison ne peux comencer que par "a" ou bien "ba" ou bien "bba"
si

={les combinaisons començant par "a"}

={les combinaisons començant par "ba"}
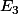
={les combinaisons començant par "bba"}
E={tt les combinaisons possible}
alors

et

=>les combinaisons començant par "a" est
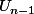
=>les combinaisons començant par "ba" est
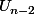
=>les combinaisons començant par "bba" est

donc
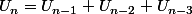
t dac avec moi??
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 01:09
par BancH » 16 Juin 2006, 01:09
Oui, j'avais pas pensé, alors l'égalité est:
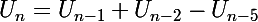
Pour tout
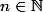
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:13
par aviateurpilot » 16 Juin 2006, 01:13
mais tu dois trouvé

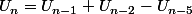
ne verifie pas ça
tu ne confirme pas ma formule
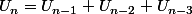
?
je l'ai fait en se basant par ta 1er methode
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 01:19
par BancH » 16 Juin 2006, 01:19
aviateurpilot a écrit: 
C'est ça qui est faux.

ou égal
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:23
par aviateurpilot » 16 Juin 2006, 01:23
=>le nombre de combinaisons de n marches commençant par a qui est égal au nombre de combinaisons de n-1 marches
=> le nombre de combinaisons començant par "ba" est
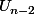
et puisque on n'a pas calculé le nombre de combinaisons començant par "bb"
si on pose

=nombre de combinaisons començant par "bb"
alors normalement
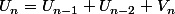
et puisque

alors

ou es la faute?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 01:26
par BancH » 16 Juin 2006, 01:26
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:29
par aviateurpilot » 16 Juin 2006, 01:29
n>4
il y a 3 possibilités
la combinaison ne peux comencer que par "a" ou bien "ba" ou bien "bba"
si

={les combinaisons començant par "a"}

={les combinaisons començant par "ba"}
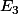
={les combinaisons començant par "bba"}
E={tt les combinaisons possible}
alors

et

=>les combinaisons començant par "a" est
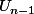
=>les combinaisons començant par "ba" est
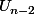
=>les combinaisons començant par "bba" est

donc
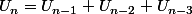
ou es la faute là?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 01:34
par BancH » 16 Juin 2006, 01:34
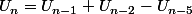
Je vais te montrer pourquoi

dans quelques minutes.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:39
par aviateurpilot » 16 Juin 2006, 01:39
quand tu me montre pour koi

montrer moi pour ça est faux:
n>4
il y a 3 possibilités
la combinaison ne peux comencer que par "a" ou bien "ba" ou bien "bba"
si

={les combinaisons començant par "a"}

={les combinaisons començant par "ba"}
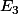
={les combinaisons començant par "bba"}
E={tt les combinaisons possible}
alors

et

=>les combinaisons començant par "a" est
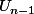
=>les combinaisons començant par "ba" est
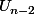
=>les combinaisons començant par "bba" est

donc
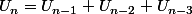
s'il est faux
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 01:40
par BancH » 16 Juin 2006, 01:40
On cherche

le nombre de combinaisons de n-2, commençant par b-b-
Pour n=6:
b-b-
=>
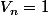
Pour n=7:
b-b-a
=>
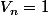
Pour n=8:
b-b-aa
=>
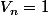
Pour n=9:
b-b-aaa
b-b-ab-
=>
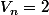
Pour n=10:
b-b-aaaa
b-b-ab-a
b-b-aab-
=>
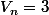
Pour n=11:
b-b-aaaaa
b-b-aaab-
b-b-aab-a
b-b-ab-b-
b-b-ab-aa
=>
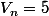
On retombe dans le cas précédent, on avait n=1, n=2... là on a n=6, n=7... avec les mêmes résultats.
Le nombre de combinaisons avec n-2 marches commençant par b-b- correspond au nombre de combinaisons totales de

marches, soit

Et il faut enlever ces

combinaisons et non les ajouter car ce sont celles qui commencent par aab-b- où aa ne peut pas être remplacé par b-
P.S. la faut que j'aille me coucher, donc on verra ça demain.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:51
par aviateurpilot » 16 Juin 2006, 01:51
"bb" dois etre forcement suivé par "a"
Mais quand elle en a monté deux (en sautant une marche)2 fois successive , ça lui file des crampes aux pattes donc elle ne monte qu'une marche au saut suivant.
et en plus j'ai dit que

est le nombre de combinaisons de n commençant par bb
et il est facile de trouvé au moin 2 combinaisons de 6 commençant par bb
mais toi t'a dit:
Pour n=6:
............
=>

=1
apart tt ca si tu revois bien cette demonstration tu va voir qu'il es 100pourcent logique et il ne se base pas sur des exemples qui peux conduire a des fautes
n>4
il y a 3 possibilités
la combinaison ne peux comencer que par "a" ou bien "ba" ou bien "bba"
si

={les combinaisons començant par "a"}

={les combinaisons començant par "ba"}
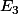
={les combinaisons començant par "bba"}
E={tt les combinaisons possible}
alors

et

=>les combinaisons començant par "a" est
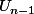
=>les combinaisons començant par "ba" est
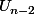
=>les combinaisons començant par "bba" est

donc
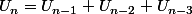
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 16 Juin 2006, 01:59
par aviateurpilot » 16 Juin 2006, 01:59
bonne nuit et à demain BancH
merci pour tt :++:
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 10:03
par BancH » 16 Juin 2006, 10:03
Là où tu as faux:
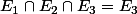
car

Pour le début de l'égalité, on est d'accord pour
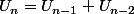
Cela représente toutes les combinaisons de n marches, or il faut exclure les combinaisons commençant par b-b-b-.
On note

le nombre de combinaisons avec n marches, et l'on met le début des combinaisons entre parenthèses.
 \Longleftrightarrow C_{n-1}(ab-b-) \Longleftrightarrow C_{n-2}(b-b-) \Longleftrightarrow C_{n-3}(ab-) \Longleftrightarrow C_{n-4}(b-) \Longleftrightarrow C_{n-5}(a) \Longleftrightarrow C_{n-6})
Donc avec
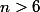
on a:
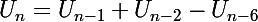
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 10:22
par BancH » 16 Juin 2006, 10:22
Mais c'est toujours faux car on a enlevé seulement les b-b-b- commençant les combinaisons, et pas les autres. Je trouve alors,
avec

le quotient de la division euclidienne de

par

:
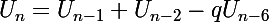
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Juin 2006, 11:07
par yos » 16 Juin 2006, 11:07
Pourquoi recommencez-vous ce problème? Il me semble qu'une solution a été donnée sur l'autre fil.
Les relations
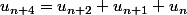
et
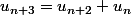
sont toutes deux correctes il me semble. La première est une conséquence immédiate de la seconde et la seconde se justifie facilement en distinguant les deux façons suivantes de gravir n+3 marches :
-celles se terminant par 1 (
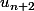
façons),
-celles se terminant par 2 et donc par 1,2 (

façons).
Si vous voyez une erreur dites le moi.
Mais peut-être cherchez-vous une formule explicite?
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 11:17
par BancH » 16 Juin 2006, 11:17
Il y a une petite différence dans l'énoncé, dans celui de Zebulon, la grenouille avait une crampe lorqu'elle montait deux marches en un saut, là, c'est lorsqu'elle monte quatre marches en deux sauts de deux marches.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Juin 2006, 12:18
par yos » 16 Juin 2006, 12:18
Ce n'est pas ce que j'avais saisi avec le premier message. Admettons.
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 16 Juin 2006, 12:22
par BancH » 16 Juin 2006, 12:22
Oui, au départ c'était la même énigme que celle posté par Zebulon mais elle a changé au cours de la discussion.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
