Zweig a écrit:Montrer que le nombre

admet strictement plus de

chiffres
La somme

a le même nombre de chiffres
que

ou alors un chiffre de plus.
Pour s'en convaincre, il suffit de remarquer, en additionnant deux entiers quelconque en base 10, qu'on ne peut pas avoir une retenue supérieure strictement à 1.
Pour avoir un ordre de grandeur de l'entier

on fait la manip suivante:
comme
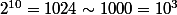
(passage de la base 2 à la base 10)
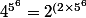}=2^{(10 \times 5^5)}=(2^{10})^{(5^5)}=10^{(3 \times 5^5)})
Le résultat a un
nombre de chiffres de l'ordre de grandeur de

ce qui n'a rien à voir avec le résultat demandé.
La somme

a 9408 ou 9409 chiffres.
La formule qui donne le nombre

de chiffres , base 10, d'un entier

:


)
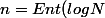+1)
où log=log base 10.
