Défilycée : Des racines cubiques.

[Kikoo <3 Bieber]

Soit

Montrer que

[Lostounet]

Soit

Montrer que

Salut !

Soit x = psi

On cherche donc un nombre x qui vérifie la relation:


Puis avec les formules de cardan, on peut essayer d'expliciter x (seule solution réelle) ! C'est un exo intéressant, et qui fait réfléchir. Et si x n'était pas la seule solution réelle de l'équation obtenue..?
Hum !

[Kikoo <3 Bieber]

Salut !

Soit x = psi

On cherche donc un nombre x qui vérifie la relation:


Puis avec les formules de cardan, on peut essayer d'expliciter x (seule solution réelle) ! C'est un exo intéressant, et qui fait réfléchir. Et si x n'était pas la seule solution réelle de l'équation obtenue..?
Hum !

Hey Lostounet !
A toi de voir si elle est unique la solution dans R En tout cas c'est déjà bien trouvé pour le début, et je sais que t'es très capable de finir l'exo proprement comme un grand !

[Lostounet]

Non, je sais bien qu'on peut passer par le th. des valeurs intermédiaires, avec croissance de la fonction, en regardant ses variations...

Mais j'envisageais plutot une généralisation du problème: Un nombre avec des racines imbriquées, mais qui ne conduit pas à un polynome "simple" (plusieurs racines réelles, difficulté à coupler le nombre avec la racine...)

[adrien69]

S'il n'y a que ça pour te faire plaisir



Avec la convention habituelle :

[Lostounet]

S'il n'y a que ça pour te faire plaisir



Avec la convention habituelle :

Tu cherches un psi complexe tel que:


Delta = -3

x1 = (1 - i;)3)/2
x2 = (1 + i;)3)/2

Lequel convient...
J'ai l'impression que c'est x1, avec ta convention.

[adrien69]

Oui, c'est bien ça la question. Lequel convient ?

[Lostounet]

Oui, c'est bien ça la question. Lequel convient ?

Je vais dire les deux ! Car nous travaillons dans C... Je me trompe?

Car les deux nombres sont tels que:

[(1 - i;)3)/2]^2 + 1 = (1 - i;)3)/2

[(1 + i;)3)/2]^2 + 1 = (1 + i;)3)/2

J'ai l'impression que la convention n'est pas i = -1 mais plutot i^2 = -1 (c'est différent)

En tout cas, si on veut jongler un peu avec les écritures de x1 et x2:

(2x1 - 1)/;)3 = -i
(2x2 - 1)/;)3 = i

Je "vois" les -1(...) qui se divisent par un 3 pour donner i ou -i
Comme le - ne peut venir du 3 :p Je vais dire que c'est i, donc peut-être bien que c'est x2. Ce n'est pas très valable comme raisonnement, je ne sais pas si c'est très mathématique...

[Dacu]

Bonsoir à tous!
Je dis que .
Cordialement!

[Archytas]

Salut Lostounet, tu sais que les solutions de l'équation x²-x-1=0 sont phi et psi et pourtant seul phi est égale aux racines imbriquées de 1. C'est parce que lorsqu'on passe au cube ou au carré on rajoute des solutions. Si ce nombre existe il n'est égale qu'à une seule racine et ne peut être égale au deux car elles sont différentes.

[Lostounet]

Et donc... comment peut-on s'en rendre compte?

[Doraki]

déjà il faudrait une définition précise de ;). Sous forme de limite et avec la convention utilisée pour les racines.

[Lostounet]

J'ai toujours pas compris ! :$

[Archytas]

J'ai toujours pas compris ! :$

Ok, je te propose une méthode barbare mais qui marche :
Tu pose on obtient le système suivant


ensuite tu montres par récurrence que je pense que ça doit suffire en disant que la chose converge vers ou son conjugué. Et si ça suffit pas on doit pouvoir aboutir en disant en plus que
Voilà, bon courage !

[adrien69]

La définition de donnée par Archytas est la bonne, comme limite, si elle existe, de la suite considérée.

Mais plutôt que de se casser le c*l à faire des calculs immondes, puisqu'on connaît déjà les résultats possibles, on va plutôt regarder comment évolue par rapport à

Avec la convention utilisée pour la racine, l'argument de vaut celui de divisé par 2.

On regarde donc les premiers arguments de la suite :



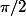
Un truc dégueulasse mais toujours positif et plus petit que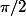
etc

Géométriquement on sent bien que les arguments vont rester dans cet intervalle. Mais pour le prouver... Eh bien en fait il faut juste écrire ce que l'on sent. C'est à dire que si l'argument de appartient à l'intervalle considéré, l'argument de est dans en tant qu'un certain barycentre de l'argument de -1 et de celui de 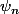(je dis un certain barycentre car il ne faut pas oublier que 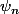n'étant pas de module 1, on ne fait pas une simple moyenne) et quand on divise par 2 on a gagné.

Ainsi à supposer que existe, son argument est dans l'intervalle qui nous permet de conclure que est dans le quart de plan supérieur droit, et que donc c'est le

Pour prouver l'existence d'une limite : le théorème de Bolzano-Weierstrass (tu le connais Lostounet ?) assure l'existence d'une suite extraite convergente.

Mais on voit que converge vers la même limite quand n tend vers l'infini, et ce, pour tout p. En travaillant par l'absurde, on peut alors montrer que 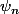ne peut posséder de sous-suite convergente.


La fin est un peu difficile et lapidaire, je l'avoue, mais je n'ai pas trop le temps.

Désolé de la latence entre le post du problème et ma réponse, quand je l'avais posé je ne voyais pas de solution et par la suite j'avais complètement oublié son existence.