Défi suite

[Archytas]

Salut,
Je viens de tomber sur un petit problème dans un magasine, je n'ai pas la réponse (ni même dans les numéros suivants ) :
On fixe et :

Siconverge c'est vers 0, mais converge-t-elle ?

[zygomatique]

salut

en tout cas la suite est bornée puisque pour n > 1 donc on peut en extraire une sous-suite convergente ...

[Matt_01]

Que vaut U_2+...+U_n ?

[Matt_01]

Bon ma réponse précédente est bien sûr inutile (j'avais pas vraiment cerné le problème).
Cependant j'ai quand même une solution qui me semble être bonne.
On remarque déja qu'on peut écrire avec dans le segment u_n et .
Maintenant, si on écrit
Alors
En posant et en utilisant la norme subordonnée à la norme 2 sur qui a le bon goût d'être sous multiplicative, on obtient que la norme de est inférieure à .

Du coup, si diverge, alors converge vers 0.
Sinon, c'est que tend vers 0 et on peut montrer que ca implique aussi que converge vers 0 (il me semble, en considérant qu'à partir d'un certain rang, [-eps,eps] a une intersection non vide avec ).

[MathieuGonzalez]

Pourquoi ne pas regarder la série de terme général Un et montrer qu'elle converge comme l'a dit Matt_01 ? Déjà en supposant U0 <= U1 on voit que c'est une série à termes positifs et qu'elle est majorée par la valeur de l'intégrale de la fonction sur R donc elle est convergente et donc la suite Un tend vers 0

[Matt_01]

Non le problème c'est que l'intégrale peut être négative, selon la position de u_n par rapport à u_(n+1).
Au passage ma démo est fausse, je me suis trompé sur la valeur de la norme des M(a_i).
Pour autant j'ai envie de dire que ca converge.

[MathieuGonzalez]

Ah oui au temps pour moi j'ai oublié de regarder ça, mais je trouvais l'idée de la somme intéressante
Une autre idée du coup ?

[Matt_01]

Néanmoins on pourrait adapter ma démo en considérant le fait que le déterminant de est . Si on arrive à montrer que les valeurs propres de sont globalement bornées (je ne sais pas si c'est vrai), on pourrait conclure que si diverge, alors converge vers 0.
Par contre faut réflechir au cas où cette somme converge.

[Matt_01]

Bon en fait je pense y arriver pour la première partie.
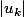
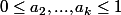
On regarde en fait pour k fixé, quel est le max de sur tq que que l'on note .
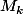
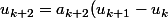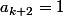
Comme , il est nécessaire de prendre pour atteindre le max.
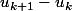
Ensuite il convient de maximiser la norme de , qui est égale à la norme de .
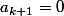
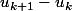
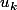
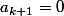
Pour maximiser cela, il est nécessaire de prendre ou 1, et donc la norme de sera soit égale à la norme de () soit à la norme de ().
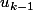
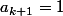
Et donc .
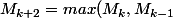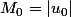
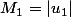
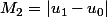
Comme , , , on en conclut que .
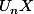
En considérant alors la norme 1 de où est vecteur propre de , on montre que toute valeur propre de est de norme inférieure à 2. On a donc ce qu'on voulait montrer.

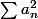
Maintenant lorsque converge, on a que tend vers 0 et donc tend vers 1.
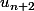
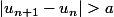
Quand on écrit sous forme d'intégrale, on remarque que si , ne peut pas s'approcher autant qu'on veut de 1 (c'est basé sur le fait que exp(-x^2) est strictement inférieure à 1 sauf en 0).
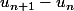
Donc tend vers 0 et donc tend vers 0 (en regardant l'expression de ).

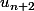
[Matt_01]

Ma première partie est vraie, cependant le fait que les valeurs propres soient bornées n'est pas suffisant, elles doivent toutes deux converger vers 0.
On peut adapter (pour la dernière fois j’espère), en écrivant que et donc :

Si on réutilise de mon message précédent, on voit que et il est assez facile de montrer que donc converge vers sa borne inf. Mais pour que cela soit faisable, il faut que la borne inf soit nulle, ou que tend vers 1, ce qui correspond à notre qui tend vers 0 et qui implique que tend vers 0.

[Lostounet]

Hello Matt,

Quelque chose m'échappe concernant tes a_n. La convergence de la suite dépend du comportement des an mais comment voir pratiquement si ça converge étant donnés U0 et U1?