Un défi pas difficile

[XzetaX]

Salut le peuple ,
Montrer que la racine cubique de 1358 n'appartient pas au corps des rationnels.
(jsais déjà comment la faire mais j'ai envie de voir qq réponses )

[Ben314]

Salut,
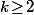
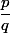
Supposons qu'un entier soit puissance -ième ( entier) d'un rationnel (sous forme irréductible) c'est à dire que . Alors divise et, comme et n'ont aucun facteur premier commun, cela n'est possible que si et donc est en fait la puissance k-ième d'un entier.

Application : Un entier se terminant par 58 est divisible par 2 mais pas par 4 donc ne peut pas être la puissance -ième d'un autre entier donc ce n'est pas non plus la puissance -iem d'un rationnel.

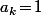
En fait, on peut même montrer un peu plus fort avec exactement la même méthode : Si (sous forme irréductible) est racine du polynôme à coefficients entier alors divise et divise . En particulier, si est unitaire (i.e. ), alors et donc est entier.