Un défi original
Olympiades mathématiques, énigmes et défis
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 07 Juin 2013, 08:16
par upium666 » 07 Juin 2013, 08:16
Bonjour à tous et à toutes !
Voilà un défi assez original, que je suis presque arrivé à résoudre :
Trouver une application
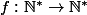
telle que :
=123...n)
ex:
=1)
=1234)
=123456789101112)
etc...
A vous de jouer :we:
-
Eurekha
- Membre Naturel
- Messages: 10
- Enregistré le: 03 Avr 2013, 13:28
-
 par Eurekha » 07 Juin 2013, 09:44
par Eurekha » 07 Juin 2013, 09:44
Bonjour,
Pour répondre à ton défi, je pars de l'écriture suivante :
=\sum_{k=1}^{n}{k10^{q}})
Le but étant de trouver q, qui dépend à la fois de

et de

.
Voici une formule qui fonctionne, il y a certainement mieux ^^ :
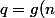-g(k),)
avec
=E(log(p))(p+1)-\frac{1}{9}10^{log(p)+1}+p+\frac{10}{9})
Eurekha
PS : J'avais établi cette formule pour calculer le fameux nombre
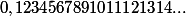
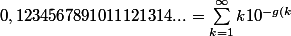}})

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 07 Juin 2013, 10:32
par Lostounet » 07 Juin 2013, 10:32
 = 1 \time 10^{n-1} + 2 \time 10^{n-2} + ... + n \time 10^0)
:blah:
P.s: pour des petits n
Ou pourquoi pas, par exemple pour générer des n<= 9
f(6) = 123456, tu ferais:
 = E( \frac{111111 \time 111111}{10^{5}} ))
En gros, n fois '1' dans les 111...1 et 10^(n-1) au dénominateur

Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités