Salut,
Soit
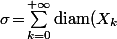)
(qu'on suppose
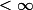
)
1) On commence par se ramener au cas d'un recouvrement d'ouverts :
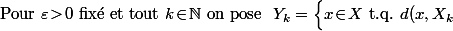\!<\!\dfrac{\varepsilon}{2^k}\Big\}=\!\!\bigcup_{x\in X_k}\!\!\!\!B\Big(x,\dfrac{\varepsilon}{2^k}\Big).)
_{k\in\N}\text{ recouvrent }X\text{ et, comme }<br />\mbox{diam}(Y_k)\!\leq\!\mbox{diam}(X_k)\!+\!2\!\times\!\dfrac{\varepsilon}{2^k},\ \text{ on a }\ \sum_{k=0}^{+\infty}\mbox{diam}(Y_k)\!\leq\!\sigma+4\varepsilon)
.
2) On considère la relation suivante : Deux éléments
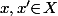
sont dit "
joignables" s'il existe une suite finie d'entier
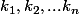
tels que
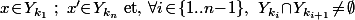
.
2.1) Dans ce cas, on a
\!\leq\!\sum_{i=1}^n\mbox{diam}(Y_{k_i})\!\leq\!\sum_{k=0}^{+\infty}\mbox{diam}(Y_k))
où la deuxième inégalité est valable à coup sûr lorsque les
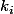
sont distincts, mais, quitte à raccourcir la suite, on peut toujours se ramener à ce cas là.
2.2) La relation en question est clairement une relation d'équivalence (la réflexivité provenant du fait que les
_{k\in\N})
recouvrent

) et, comme les
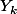
sont ouverts, les classes d'équivalence pour cette relation sont ouvertes donc elles sont aussi fermées vu qu'une classe c'est le complémentaire de la réunion de toutes les autres. Comme

est connexe, il y a donc une seule classe ce qui signifie que deux éléments quelconques
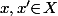
sont toujours
joignables donc tels que
\!\leq\!\sigma\!+\!4\varepsilon)
.
Ceci étant vrai pour tout
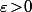
, c'est que
\!\leq\!\sigma)
et donc
\!\leq\!\sigma)
.
