Un defi CONTRE intuitif

[windows7]

salut,
nightmare m'a donné une idée, jvous propose un ptit exo dont le resultat est carrément contre intuitif.


on se place dans IR^n

trouvez le n tq la surface de l'hypersphere soit maximale.

[Ben314]

Salut,
Deux questions :
1) L'hypersphère, c'est les X tels que ||X||=R pour la norme euclidienne dont on mesure la longueur si on est dans R², la surface dans R^3,... la mesure de dimension n-1 lorsque l'on est dans R^n ?
2) Ton hypersphère, on la prend de quel rayon ?

[Nightmare]

Pour la sphère unité, on dérive la formule du volume, je trouve avec un bon logiciel n=7.

[windows7]

Salut,
Deux questions :
1) L'hypersphère, c'est les X tels que ||X||=R pour la norme euclidienne dont on mesure la longueur si on est dans R², la surface dans R^3,... la mesure de dimension n-1 lorsque l'on est dans R^n ?
2) Ton hypersphère, on la prend de quel rayon ?

salut bien,

1) on prend la norme 2, l'hypersphere unitaire c'est x1²+.. xn²=1
2) on la prend unitaire donc.


>>nightmare : oui c'est 7, etonnant non ?

[mathelot]

Bj,

dans les sphères, il y en a trois (et 3 seulement) qui sortent du lot:

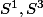et 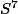qui ont des structures de
groupe de Lie différentiable. je ne sais s' il y a un lien

p-e , vû que plus c'est régulier, plus ça maximise (rectangle versus carré par exemple)

@window: celle qui maximise l'aire c'est la boule de R7
donc en fait, c'est ça ?

je vois pas trop comment on peut regarder. Comme le souligne Night,
les boules s'injectent les unes dans les autres, et inversement se retrouvent par projection sur l'axe de dernière coordonnée.
Dès lors, les groupes spéciaux unitaires s'injectent aussi .

la mesure d'aire et de volume de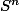 sont invariantes par les isométries (???)

[ffpower]

Je ne pense pas qu'il y ait de regard géométrique pertinent à avoir : le prob dans cette question est qu'on compare des trucs pas homogenes ( du coup ça dépend du rayon choisi au départ ). C'est un peu comme si je me demandais qu'est ce qui est le plus grand entre la surface de mon appart et la distance que je parcours pour aller au boulot..Mais si on tiens vraiment à avoir un regard géométrique, par exemple quand on compare le disque unité et la boule unité, il faut faire en sorte de se ramener à des objets de même type : donc qu'est ce qui est le plus grand entre la boule unité et un cylindre de hauteur 1 et de base un disque unité..Mais du coup là, ya plus d'injections naturelles de l'un dans l'autre..

[Ericovitchi]

C'est quoi que tu as dérivé ? c'est ?
donc la surface c'est ?



Effectivement, c'est comme ça que tu as trouvé 7.

[windows7]

mathelot : t'as regardé le sujet de nightmare sur le volume ? partant de la c'est assez simple ..

[windows7]

ericovitchi : moi j'ai gamma(n/2) ( ? )

Edit : c'est bon, on a pa la meme ecriture

[mathelot]

Je ne pense pas qu'il y ait de regard géométrique pertinent à avoir : le prob dans cette question est qu'on compare des trucs pas homogenes ( du coup ça dépend du rayon choisi au départ ). C'est un peu comme si je me demandais qu'est ce qui est le plus grand entre la surface de mon appart et la distance que je parcours pour aller au boulot..Mais si on tiens vraiment à avoir un regard géométrique, par exemple quand on compare le disque unité et la boule unité, il faut faire en sorte de se ramener à des objets de même type : donc qu'est ce qui est le plus grand entre la boule unité et un cylindre de hauteur 1 et de base un disque unité..Mais du coup là, ya plus d'injections naturelles de l'un dans l'autre..

"philosophiquement", je suis pas trop d'accord. je préfère penser
que "faire varier continuement" la dimension est un sujet inexploré
(cf dimension fractale,courbe de Péano). Dans l'expérience concrête, quand on dessine
trop nerveusement une courbe de fonction réelle au crayon, ça devient petit à petit une courbe fractale puis une surface

d'ailleurs question:
certains contributeurs écrivent des n! (discrets ) et d'autres des continues. Mais ,y a t il des espaces topologiques
mesurés dont le bord a une aire non entière donnée par la formule plus haut ?

de plus, la dimension qui donne le maximum n'est pas entière :we:

[JeanJ]

Tien ! je n'avais pas vu ce "défi" !
Si non j'aurai donné tout de suite cette référence, où tout y est :
http://mathworld.wolfram.com/Hypersphere.html
Et pour ceux qui veulent aller encore un peu plus loin, cet article (bien que le vocabulaire employé ne soit pas toujours le meilleur) :
"Le problème de l'hyperchèvre" par le lien :
http://www.scribd.com/JJacquelin/documents