Bonjour à tous.
4/409 peut il être décomposé en la somme de 3 inverses d'entiers 1/a+1/b+1/c ?
Bonne recherche
Décomposition d'une fraction
8 messages
- Page 1 sur 1
C'est une équation diophantienne. Je vois plusieurs cas.
Pour chaque dénominateur a,b,c, soit 409 est un diviseur auquel cas, par ex}{409})
Soit 409 n'est pas un diviseur et par ex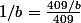
Donc en gros la question, c'est, en sommant 3 termes de la forme 1/k ou de la forme 409/h pour des entiers k,h, peut-on faire 4 ?
Déjà, si les trois termes sont de la forme 1/k, c'est impossible, on fait 3 max.
Si j'en ai deux de la forme 1/k, j'obtiens que l'entier du terme en 409/k s'écrit comme un quotient de 409 par 4- 1/k1-1/k2
Ce qui donne 409k1k2 = k(4k1k2-k1-k2).
Si 409 divise k, alors 409/k est de la forme 1/k' et on revient au cas précédant.
Donc 409 divise 4k1k2-k1-k2 et après...
EDIT : Je sais qu'il y a eu une équation diophantienne proche de celle-ci récemment mais je ne l'ai pas retrouvé. N'ayant jamais fait de théorie des nombres, je sèche.
Pour chaque dénominateur a,b,c, soit 409 est un diviseur auquel cas, par ex
Soit 409 n'est pas un diviseur et par ex
Donc en gros la question, c'est, en sommant 3 termes de la forme 1/k ou de la forme 409/h pour des entiers k,h, peut-on faire 4 ?
Déjà, si les trois termes sont de la forme 1/k, c'est impossible, on fait 3 max.
Si j'en ai deux de la forme 1/k, j'obtiens que l'entier du terme en 409/k s'écrit comme un quotient de 409 par 4- 1/k1-1/k2
Ce qui donne 409k1k2 = k(4k1k2-k1-k2).
Si 409 divise k, alors 409/k est de la forme 1/k' et on revient au cas précédant.
Donc 409 divise 4k1k2-k1-k2 et après...
EDIT : Je sais qu'il y a eu une équation diophantienne proche de celle-ci récemment mais je ne l'ai pas retrouvé. N'ayant jamais fait de théorie des nombres, je sèche.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
